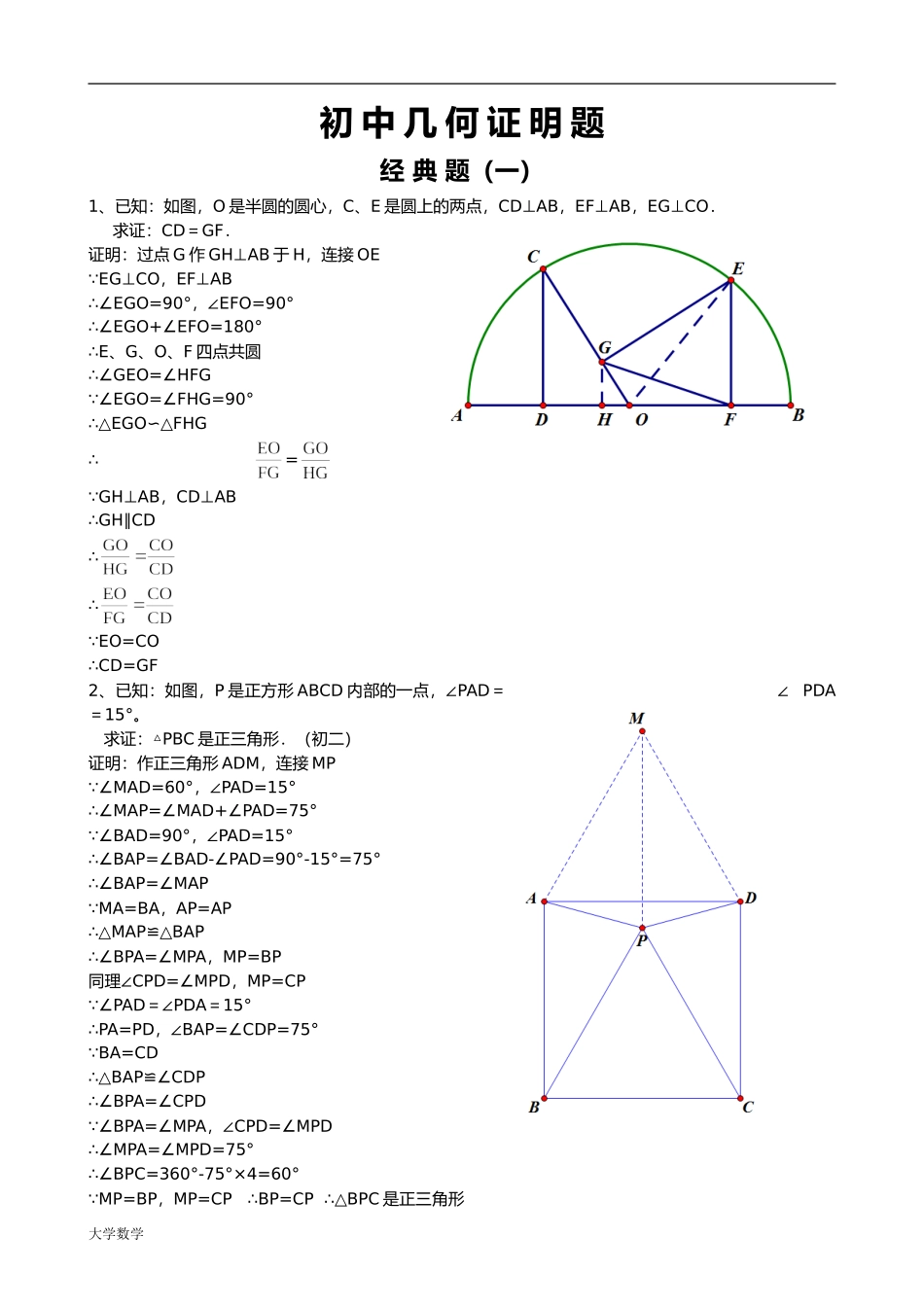
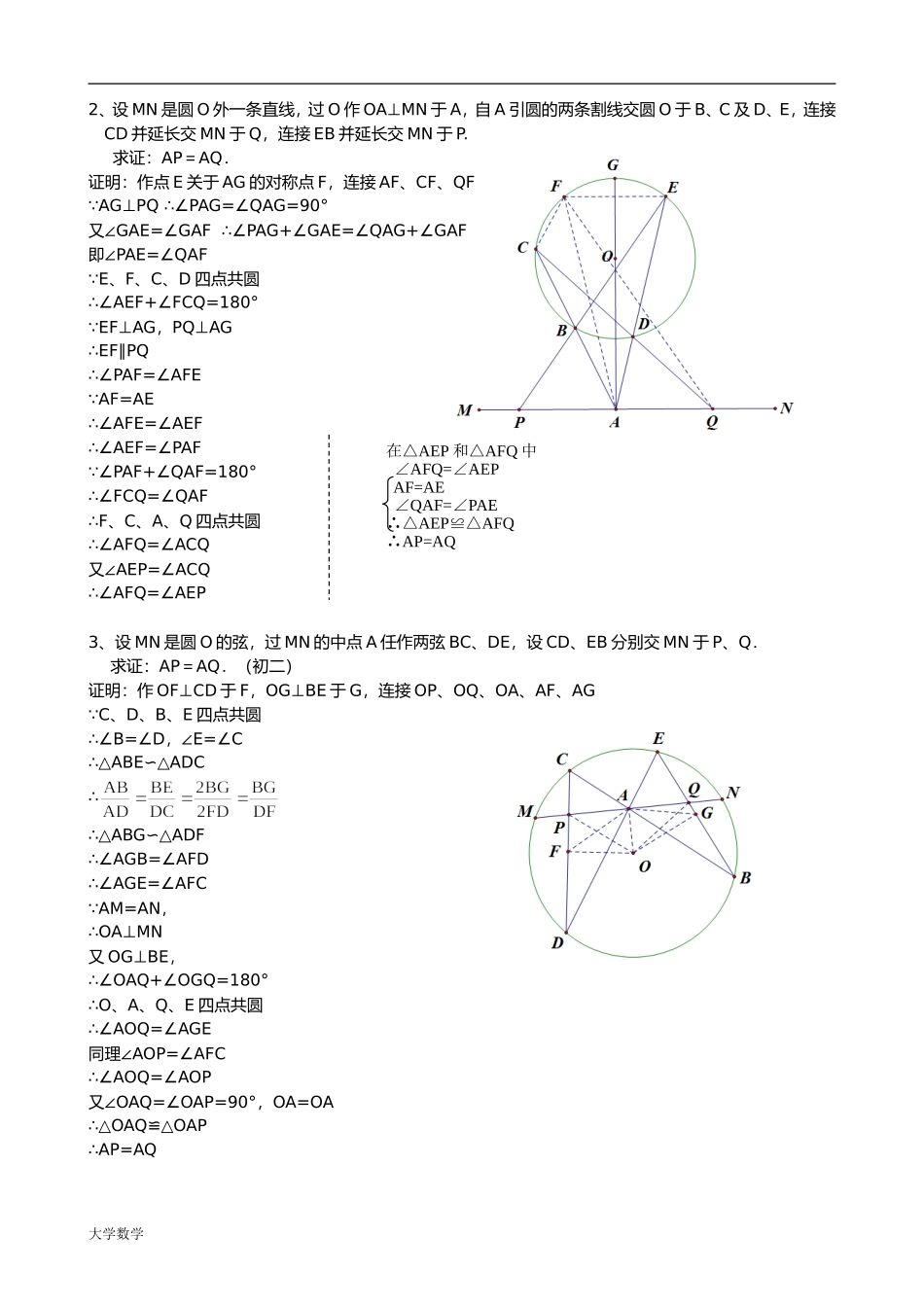
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.证明:过点G作GH⊥AB于H,连接OE EG⊥CO,EF⊥AB∴∠EGO=90°,∠EFO=90°∴∠EGO+∠EFO=180°∴E、G、O、F四点共圆∴∠GEO=∠HFG ∠EGO=∠FHG=90°∴△EGO∽△FHG∴= GH⊥AB,CD⊥AB∴GH∥CD∴∴ EO=CO∴CD=GF2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°。求证:△PBC是正三角形.(初二)证明:作正三角形ADM,连接MP ∠MAD=60°,∠PAD=15°∴∠MAP=∠MAD+∠PAD=75° ∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75°∴∠BAP=∠MAP MA=BA,AP=AP∴△MAP≌△BAP∴∠BPA=∠MPA,MP=BP同理∠CPD=∠MPD,MP=CP ∠PAD=∠PDA=15°∴PA=PD,∠BAP=∠CDP=75° BA=CD∴△BAP≌∠CDP∴∠BPA=∠CPD ∠BPA=∠MPA,∠CPD=∠MPD∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60° MP=BP,MP=CP∴BP=CP∴△BPC是正三角形大学数学3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.证明:连接AC,取AC的中点G,连接NG、MG CN=DN,CG=DG∴GN∥AD,GN=AD∴∠DEN=∠GNM AM=BM,AG=CG∴GM∥BC,GM=BC∴∠F=∠GMN AD=BC∴GN=GM∴∠GMN=∠GNM∴∠DEN=∠F经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)证明:(1)延长AD交圆于F,连接BF,过点O作OG⊥AD于G OG⊥AF∴AG=FG AB=AB∴∠F=∠ACB又AD⊥BC,BE⊥AC∴∠BHD+∠DBH=90°∠ACB+∠DBH=90°∴∠ACB=∠BHD∴∠F=∠BHD∴BH=BF又AD⊥BC∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH)=2GD又AD⊥BC,OM⊥BC,OG⊥AD∴四边形OMDG是矩形∴OM=GD∴AH=2OM(2)连接OB、OC ∠BAC=60∴∠BOC=120° OB=OC,OM⊥BC∴∠BOM=∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM∴AH=BO=AO大学数学2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.证明:作点E关于AG的对称点F,连接AF、CF、QF AG⊥PQ∴∠PAG=∠QAG=90°又∠GAE=∠GAF∴∠PAG+∠GAE=∠QAG+∠GAF即∠PAE=∠QAF E、F、C、D四点共圆∴∠AEF+∠FCQ=180° EF⊥AG,PQ⊥AG∴EF∥PQ∴∠PAF=∠AFE AF=AE∴∠AFE=∠AEF∴∠AEF=∠PAF ∠PAF+∠QA...