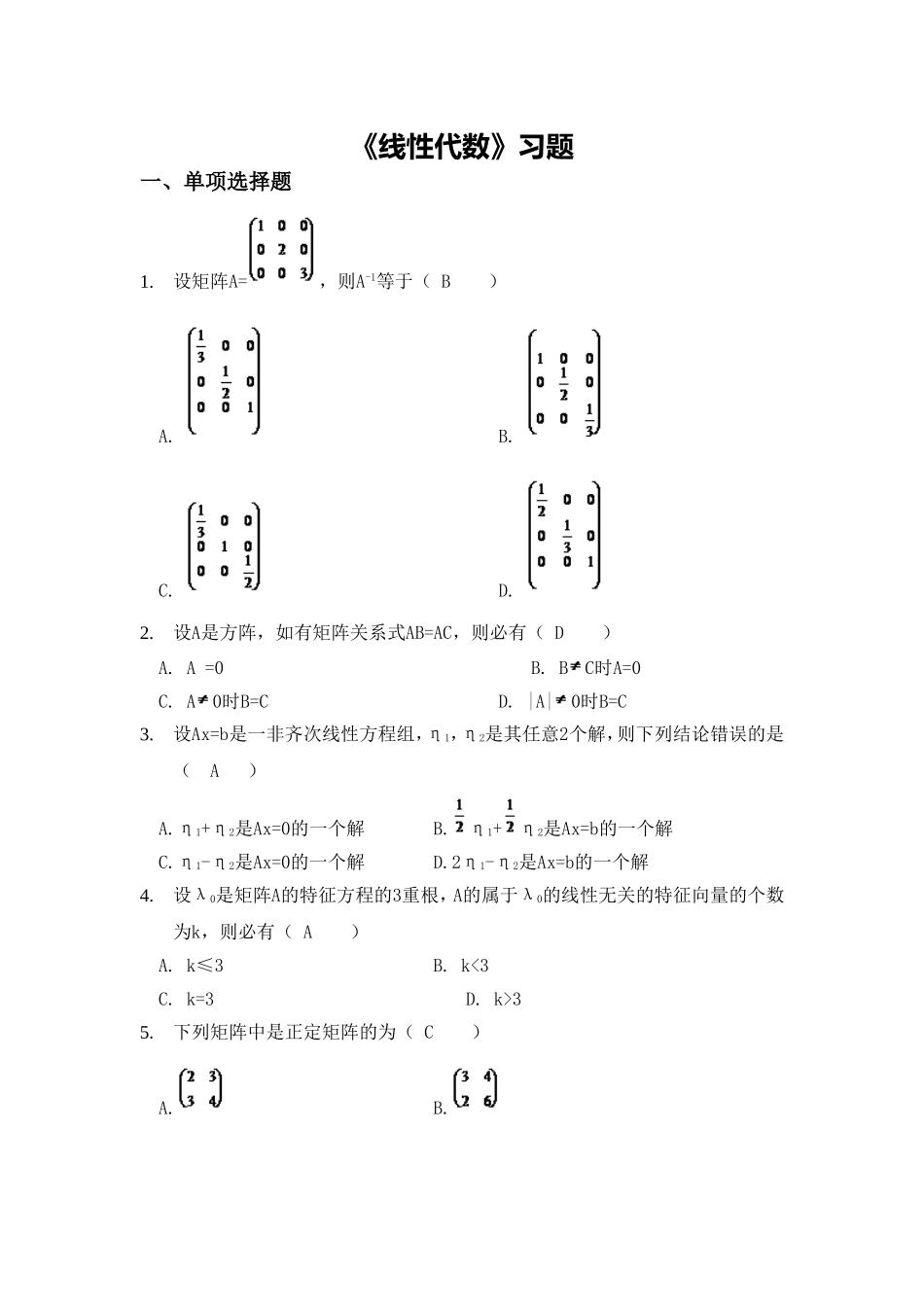
《线性代数》习题一、单项选择题1.设矩阵A=,则A-1等于(B)A.B.C.D.2.设A是方阵,如有矩阵关系式AB=AC,则必有(D)A.A=0B.BC时A=0C.A0时B=CD.|A|0时B=C3.设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是(A)A.η1+η2是Ax=0的一个解B.η1+η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解4.设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有(A)A.k≤3B.k<3C.k=3D.k>35.下列矩阵中是正定矩阵的为(C)A.B.C.D.6.下列矩阵中,(B)不是初等矩阵。A.B.C.D.7.设向量组线性无关,则下列向量组中线性无关的是(D)。A.B.C.D.8.设A为n阶方阵,且。则(C)A.B.C.D.9.设为矩阵,则有(D)。A.若,则有无穷多解;B.若,则有非零解,且基础解系含有个线性无关解向量;C.若有阶子式不为零,则有唯一解;D.若有阶子式不为零,则仅有零解。10.若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则(A)A.A与B相似B.,但|A-B|=0C.A=BD.A与B不一定相似,但|A|=|B|11.已知矩阵,则(C)12.设四阶行列式,则其中x的一次项的系数为(A)(A)1(B)-1(C)2(D)-213.设分块矩阵,其中的子块A1,A2为方阵,O为零矩阵,若A可逆,则(C)(A)A1可逆,A2不一定可逆(B)A2可逆,A1不一定可逆(C)A1,A2都可逆(D)A1,A2都不一定可逆14.用初等矩阵左乘矩阵,相当于对A进行如下何种初等变换(B)(A)(B)(C)(D)15.非齐次线性方程组在以下哪种情形下有无穷多解.(C)(A)(B)(C)(D)16.设矩阵A,B,C,X为同阶方阵,且A,B可逆,AXB=C,则矩阵X=(A)A.A-1CB-1B.CA-1B-1C.B-1A-1CD.CB-1A-117.设是四维向量,则(B)A.一定线性无关B.一定线性相关C.一定可以由线性表示D.一定可以由线性表出18.设A是n阶方阵,若对任意的n维向量x均满足Ax=0,则(A)A.A=0B.A=EC.r(A)=nD.0