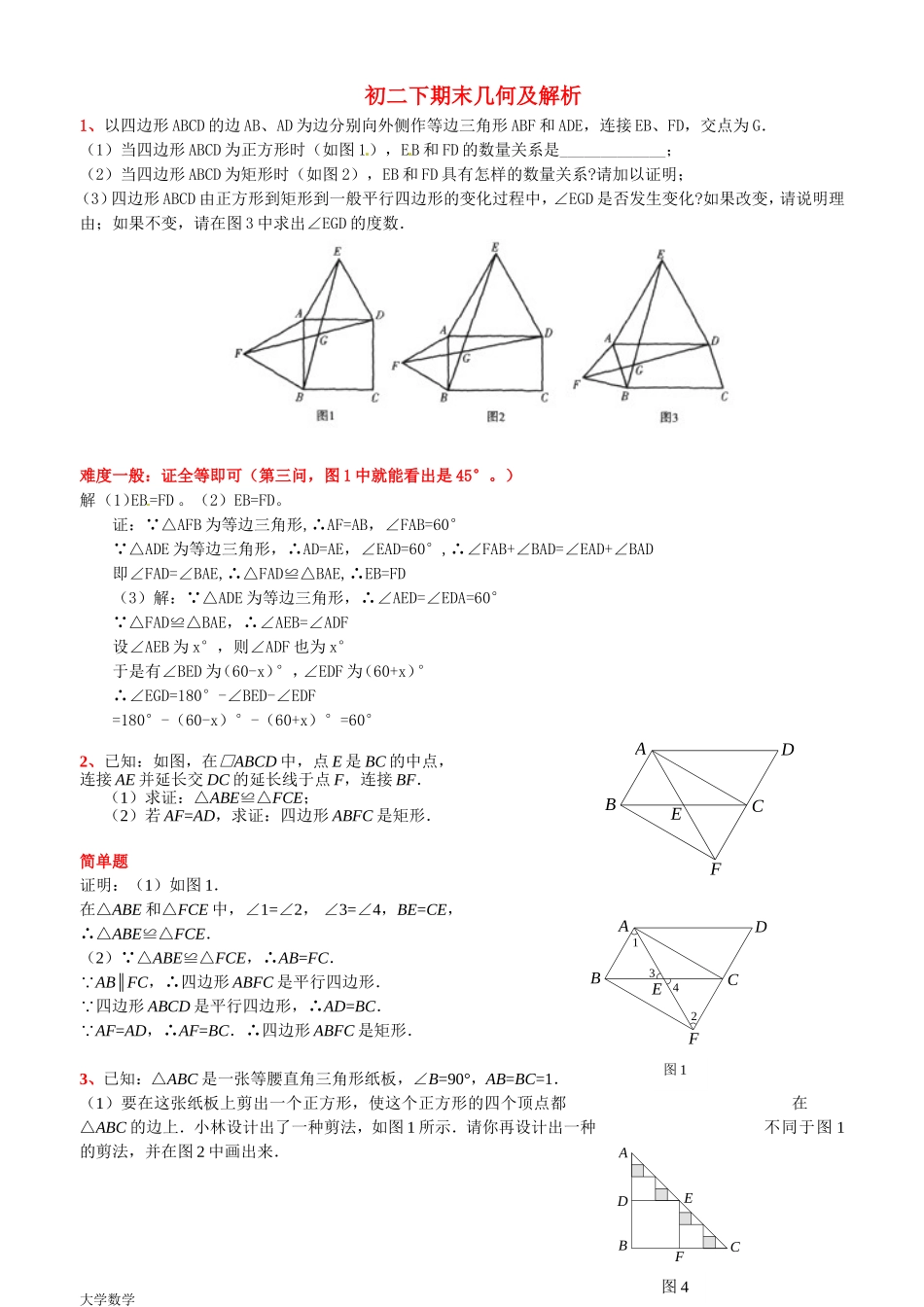
初二下期末几何及解析1、以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是_____________;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.难度一般:证全等即可(第三问,图1中就能看出是45°。)解(1)EB=FD。(2)EB=FD。证: △AFB为等边三角形,∴AF=AB,∠FAB=60° △ADE为等边三角形,∴AD=AE,∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD即∠FAD=∠BAE,∴△FAD≌△BAE,∴EB=FD(3)解: △ADE为等边三角形,∴∠AED=∠EDA=60° △FAD≌△BAE,∴∠AEB=∠ADF设∠AEB为x°,则∠ADF也为x°于是有∠BED为(60-x)°,∠EDF为(60+x)°∴∠EGD=180°-∠BED-∠EDF=180°-(60-x)°-(60+x)°=60°2、已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:△ABE≌△FCE;(2)若AF=AD,求证:四边形ABFC是矩形.简单题证明:(1)如图1.在△ABE和△FCE中,∠1=∠2,∠3=∠4,BE=CE,∴△ABE≌△FCE.(2) △ABE≌△FCE,∴AB=FC. AB∥FC,∴四边形ABFC是平行四边形. 四边形ABCD是平行四边形,∴AD=BC. AF=AD,∴AF=BC.∴四边形ABFC是矩形.3、已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.大学数学图4ABCFEDFABCDE图14321EDCBAF(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为,则=___________;余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为,则=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为;按照同样的方法继续操作下去……,第次裁剪得到_________个新的正方形,它们的面积的和=______________.(题外题:把你剪出的正方形的面积与图1中的正方形面积进行比较。)本题相当于中考12题的简单题解:(1)如图2;--...