复旦大学《大学物理》课件-卡诺循环(1).pptxVIP免费

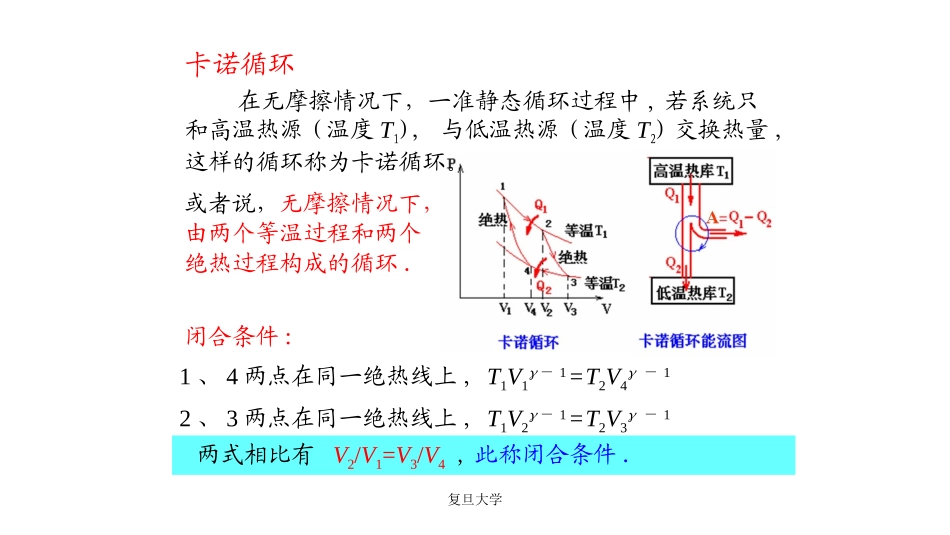
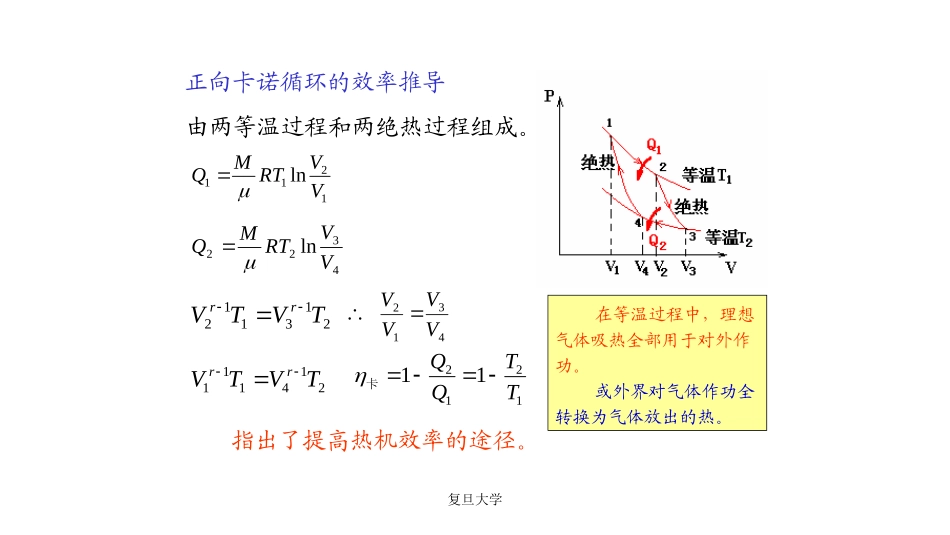
卡诺循环复旦大学卡诺循环或者说，无摩擦情况下，由两个等温过程和两个绝热过程构成的循环.在无摩擦情况下，一准静态循环过程中,若系统只和高温热源(温度T1),与低温热源(温度T2)交换热量,这样的循环称为卡诺循环。闭合条件:1、4两点在同一绝热线上,T1V1－1=T2V4－12、3两点在同一绝热线上,T1V2－1=T2V3－1两式相比有V2/V1=V3/V4,此称闭合条件.复旦大学由两等温过程和两绝热过程组成。1211lnVVRTMQ4322lnVVRTMQ正向卡诺循环的效率推导213112TVTVrr214111TVTVrr121211TTQQ卡指出了提高热机效率的途径。4312VVVV在等温过程中，理想气体吸热全部用于对外作功。或外界对气体作功全转换为气体放出的热。复旦大学现代“标准火力发电厂”：KTCt853580101KTCt30330202...