湖南大学《高等数学》课件-第1章集合与函数.pdfVIP免费

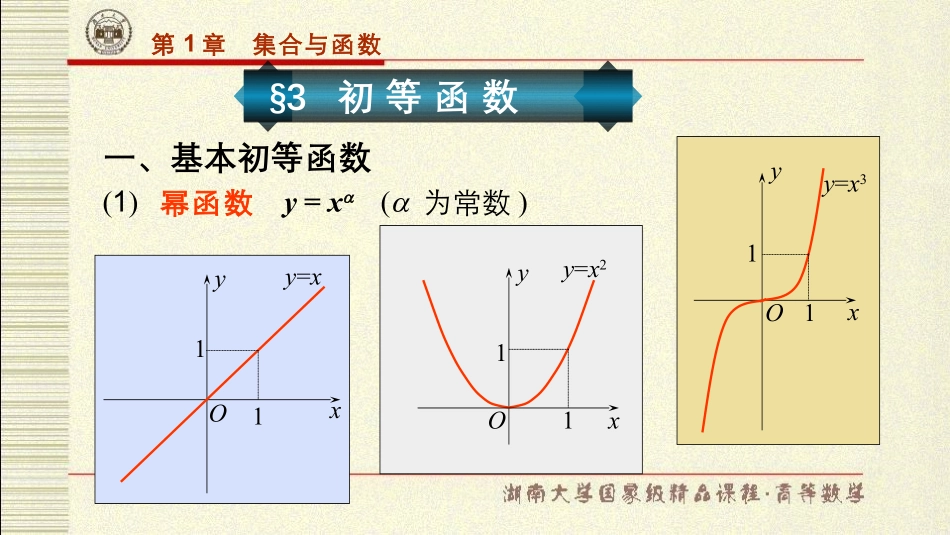
第第11章章集合与函数集合与函数第1章集合与函数§3初等函数一、基本初等函数y=xO11xyy=x2O1xy1O1xy=x3y1(1)幂函数y=x(为常数)第1章集合与函数O1xy1xyOyxxy11132xyxyO11121xyxO1y第1章集合与函数(2)指数函数y=ax(a>0,a≠1为常数)(e=2.718281828459045…)(3)对数函数y=logax(a>0,a≠1为常数)例2y=log10x=lgx(常用对数)y=logex=lnx(自然对数)例1y=exxyO1y=axa>1a<1xyO1y=logaxa>1a<1第1章集合与函数(4)三角函数x.yx,yx,yx,yx,yx,ycscseccottancossin2－1O2232－1y=sinxyxy=cosx2－2232－1xyO1第1章集合与函数xOy=tanx22232yxOy=cotx22232y第1章集合与函数(5)反三角函数x,yx,yx,yarctanarccosarcsinx.ycotarc2－1O1y=arcsinxxy2－2...