国防科技大学《高等数学》课件-第8章.pdfVIP免费

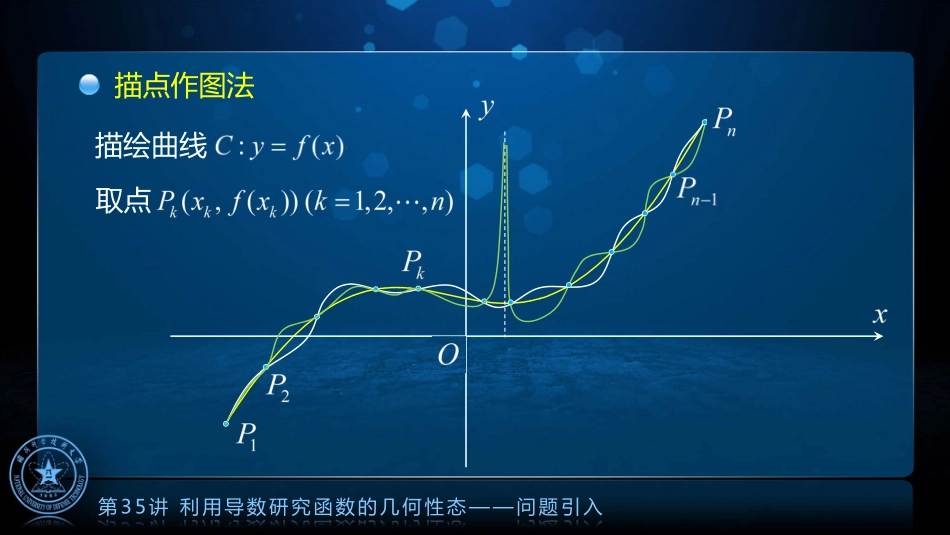
第35讲利用导数研究函数的几何性态——问题引入描点作图法描绘曲线取点第35讲利用导数研究函数的几何性态——主要内容函数图形的几何性态回顾函数图形的渐近线函数的几何性态研究第35讲利用导数研究函数的几何性态——函数图形的几何性态回顾函数图形特性条件结论示例增减性凹凸性()0fx()fx增()0fx()fx减()0fx()fx下凸(凹)()0fx()fx上凸(凸)第35讲利用导数研究函数的几何性态——函数图形的几何性态回顾点的类型极值点与拐点判定方法示例0()fxx在两侧异号00()0,()0fxfx0x极值点00(,())xfx拐点0()fxx在两侧异号00()0,()0fxfx第35讲利用导数研究函数的几何性态——函数图形的渐近线xyO51015-5-10-15()arctanfxx0,2yy变化趋势——接近水平直线第35讲利...