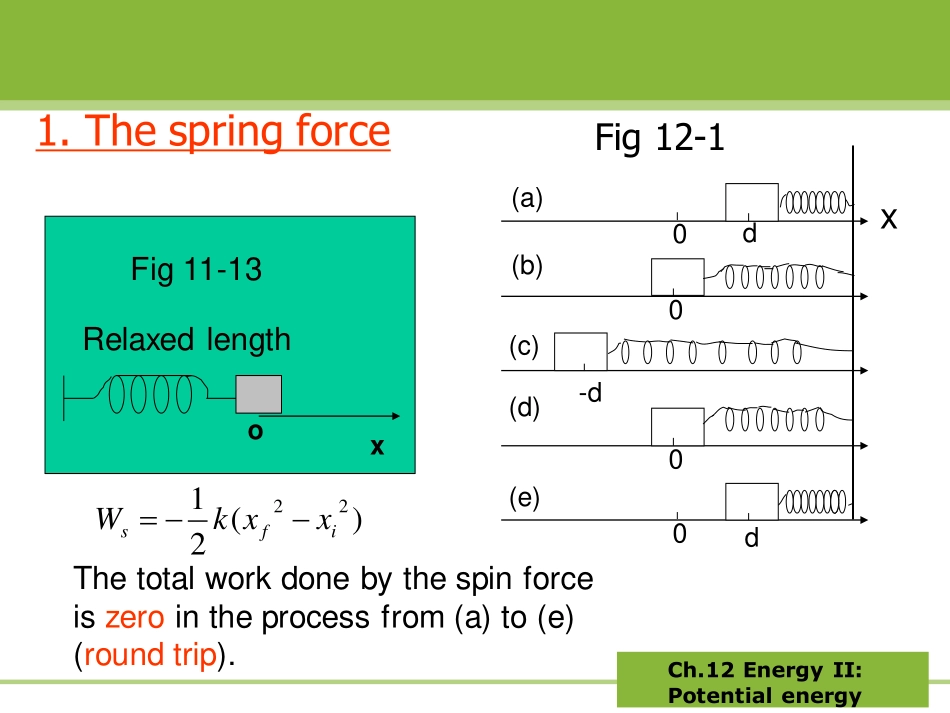
Ch.12EnergyII:PotentialenergyCh.12EnergyII:PotentialenergyCh.12EnergyII:Potentialenergy12-1Conservativeforces(保守力)Potentialenergy?Itisdefinedonlyforacertainclassofforcescalledconservativeforces.Dospringforce,gravitationalforce,andfrictionalforceetal.belongtoconservativeforces?KineticenergyVelocityWhatareconservativeforces?Ch.12EnergyII:Potentialenergy1.ThespringforceFig12-1x00dd-d(a)(b)(c)(d)(e))(2122ifsxxkW−−=oxRelaxedlengthFig11-13Thetotalworkdonebythespinforceiszerointheprocessfrom(a)to(e)(roundtrip).00Ch.12EnergyII:PotentialenergyThetotalworkdonebythegravityiszeroduringtheroundtrip.2.TheforceofgravityIfthegravitationalforceisnotconstant,istherest...