华东师范大学《高等数学》课件-第四章中.pdfVIP免费

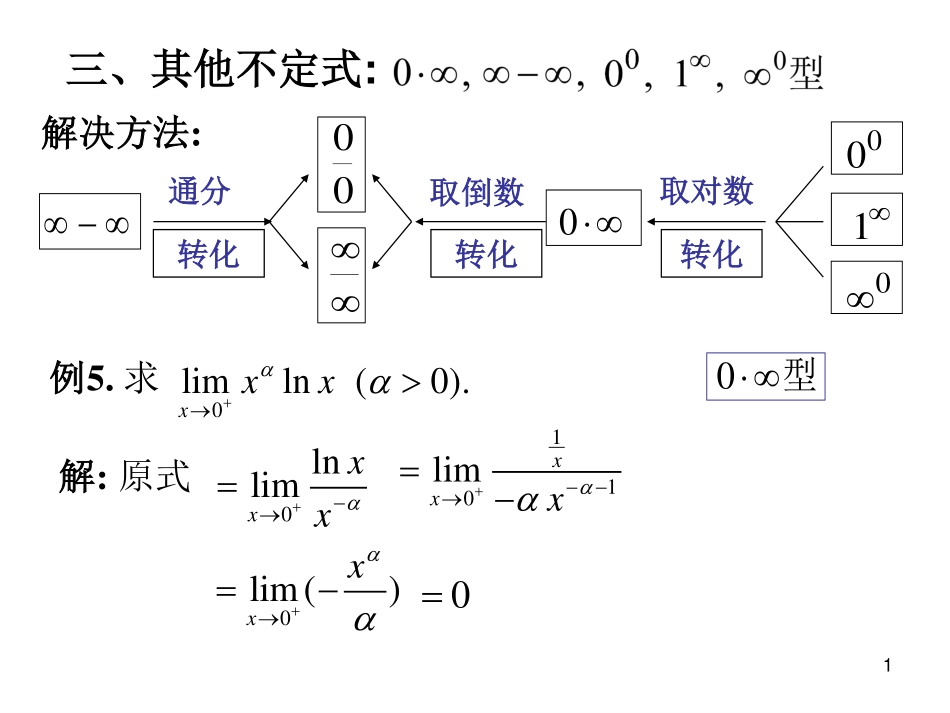
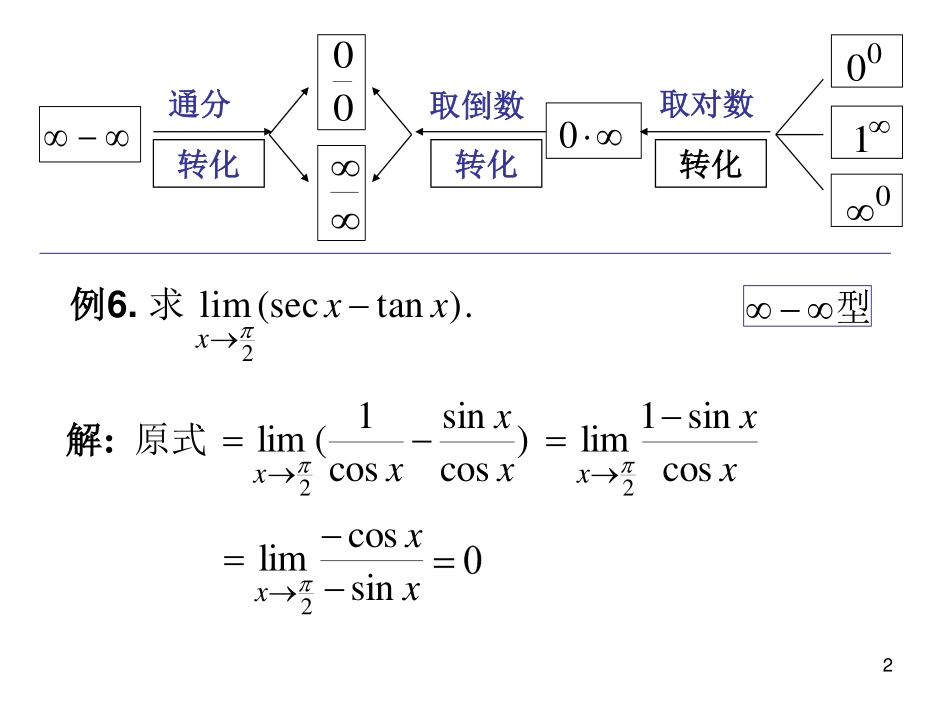
华东师范大学高等数学����1三、其他不定式:解决方法:通分转化000取倒数转化0010取对数转化例5.求0limln(0).xxx型0解:原式0lnlimxxx110limxxx00lim()xx2型.)tan(seclim2xxx解:原式)cossincos1(lim2xxxxxxxcossin1lim2xxxsincoslim2例6.求通分转化000取倒数转化0010取对数转化3例7.求.lim0xxx型00解:xxx0limxxxeln0lim0e1利用例5通分转化000取倒数转化0010取对数转化4例8.求.sintanlim20xxxxx解:注意到～原式30tanlimxxxx22031seclimxxx2203tanlimxxxxx22tan1sec31型005内容小结洛必达法则型00,1,0型...