湖南大学《高等数学》课件-第2章.pdfVIP免费

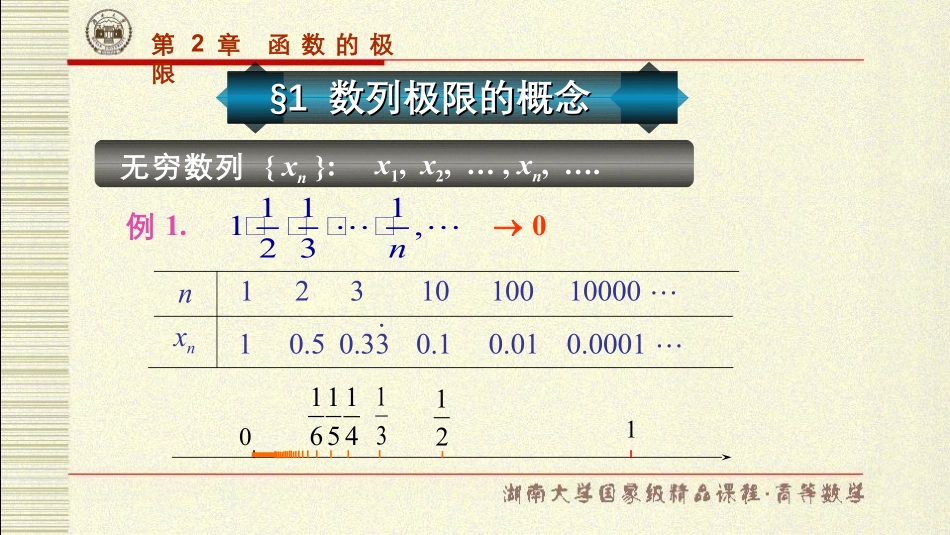
第第22章章函数的极限函数的极限例1.,131211n，，，，1231010010000nxn0.10.010.000110.50.33.2131415161010无穷数列{xn}:§1§1数列极限的概念数列极限的概念x1,x2,…,xn,….第2章函数的极限,)1(1,544532,230nn，，，，例2.123451011100101nxn1.101.51.250.81.010.9090..0.9900...0.662367453254027611第2章函数的极限,21,814121n，，，例3.例4.0.3，0.33，0.333，…，0.33…3,…n个31→0给定数列{xn},当n无限增大时,xn无限地趋近于某一个常数a.称a为{xn}的极限,并称{xn}收敛,记为.limaxnn,01limnn,1])1(1[limnnn,021limnn一尺之棰,日取其半,万世不竭.(《庄子·天下篇》).31)103103103(lim2nn第2章函数的极限例5.1，3，5，，2n－1，...