华东师范大学《高等数学》课件-第三章上.pdf

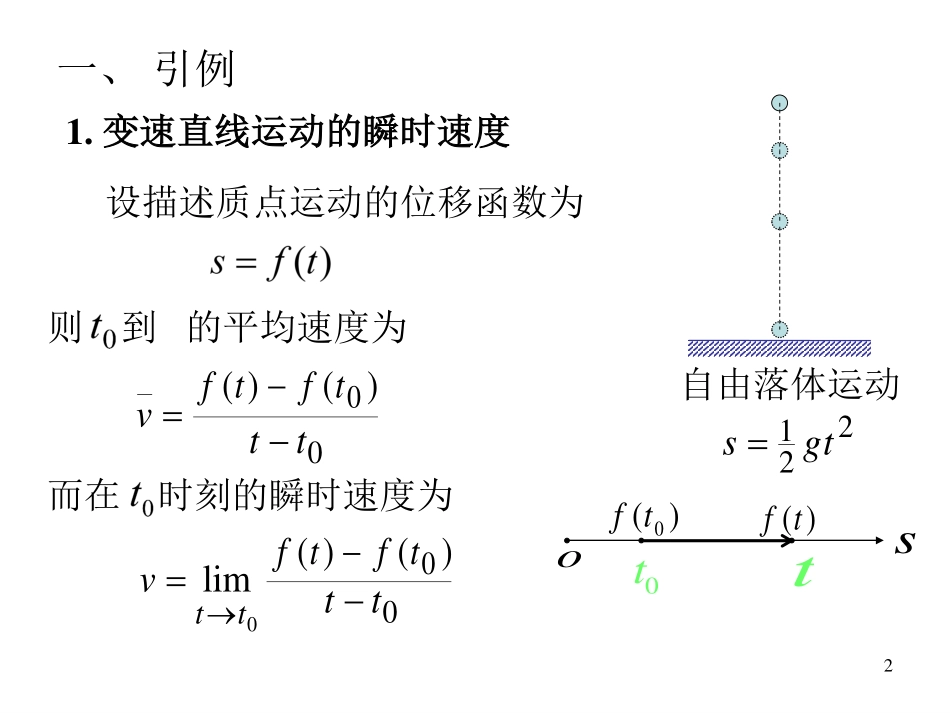
华东师范大学高等数学����第三章微积分学的创始人:德国数学家Leibniz微分学导数描述函数变化快慢微分描述函数变化程度都是描述物质运动的工具(从微观上研究函数)导数与微分英国数学家Newton1一、引例1.变速直线运动的瞬时速度设描述质点运动的位移函数为0t则到的平均速度为v)()(0tftf0tt而在时刻的瞬时速度为lim0ttv)()(0tftf0tt221tgsso)(0tf)(tft自由落体运动2xyo)(xfyC2.曲线的切线斜率曲线NT0xM在M点处的切线x割线MN的极限位置MT(当时)割线MN的斜率tan)()(0xfxf0xx切线MT的斜率tanlimlim0xxk)()(0xfxf0xx3两个问题的共性:so0t)(0tf)(tf瞬时速度切线斜率xyo)(xfyCNT0xMx所求量为函数增量与自变量增量之比的极限.类似问题还有:加速度角速度线密度电...