双曲线简单的几何性质PPT课件.pptVIP免费

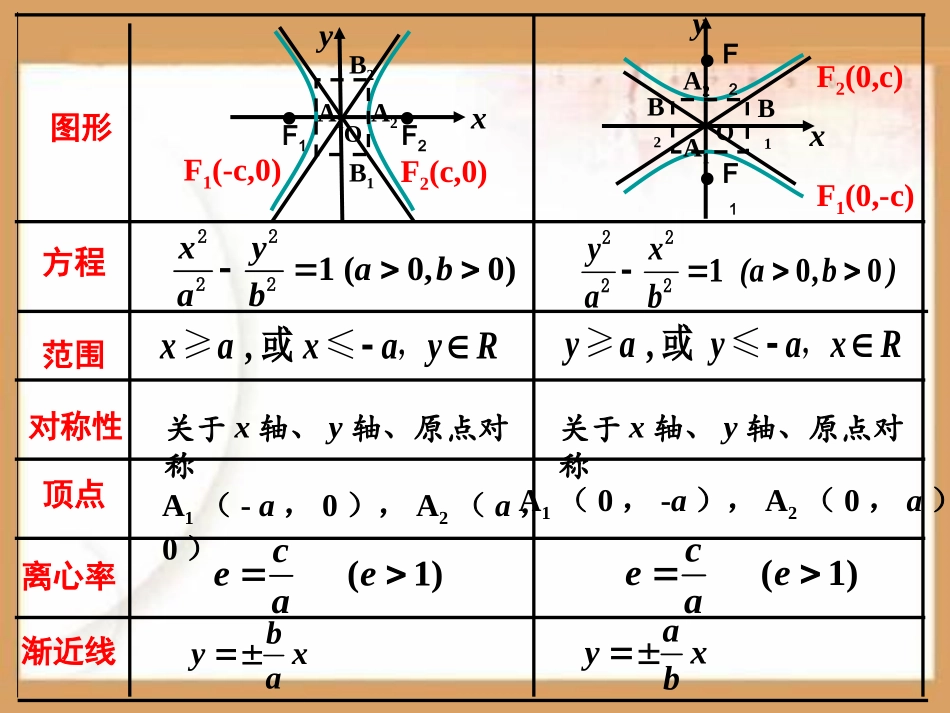
双曲线简单的几何性质(二)双曲线的第二定义关于x轴、y轴、原点对称图形方程范围对称性顶点离心率1(0,0)xyabab2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）100yx(a,b)ab2222,yayaxR≥≤，或关于x轴、y轴、原点对称(1)ceea渐近线ayxb..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c),xaxayR≥≤，或(1)ceeabyxaoxy解：4,2)x21y4xM（的交于＝与渐近线＝点作直线过Q321,2Myxx点在直线＝的下方，即双曲线焦点在轴上2222100(,)xyabab设双曲线方程为得到入上式代），把双曲线经过点（,)3,4(34,1,4)2),122ba解得由例1.已知双曲线的渐近线是，并且双曲线过点02yx)3,4(M,求双曲线方程。Q4M2222431()ab1)12yx又渐近线是...