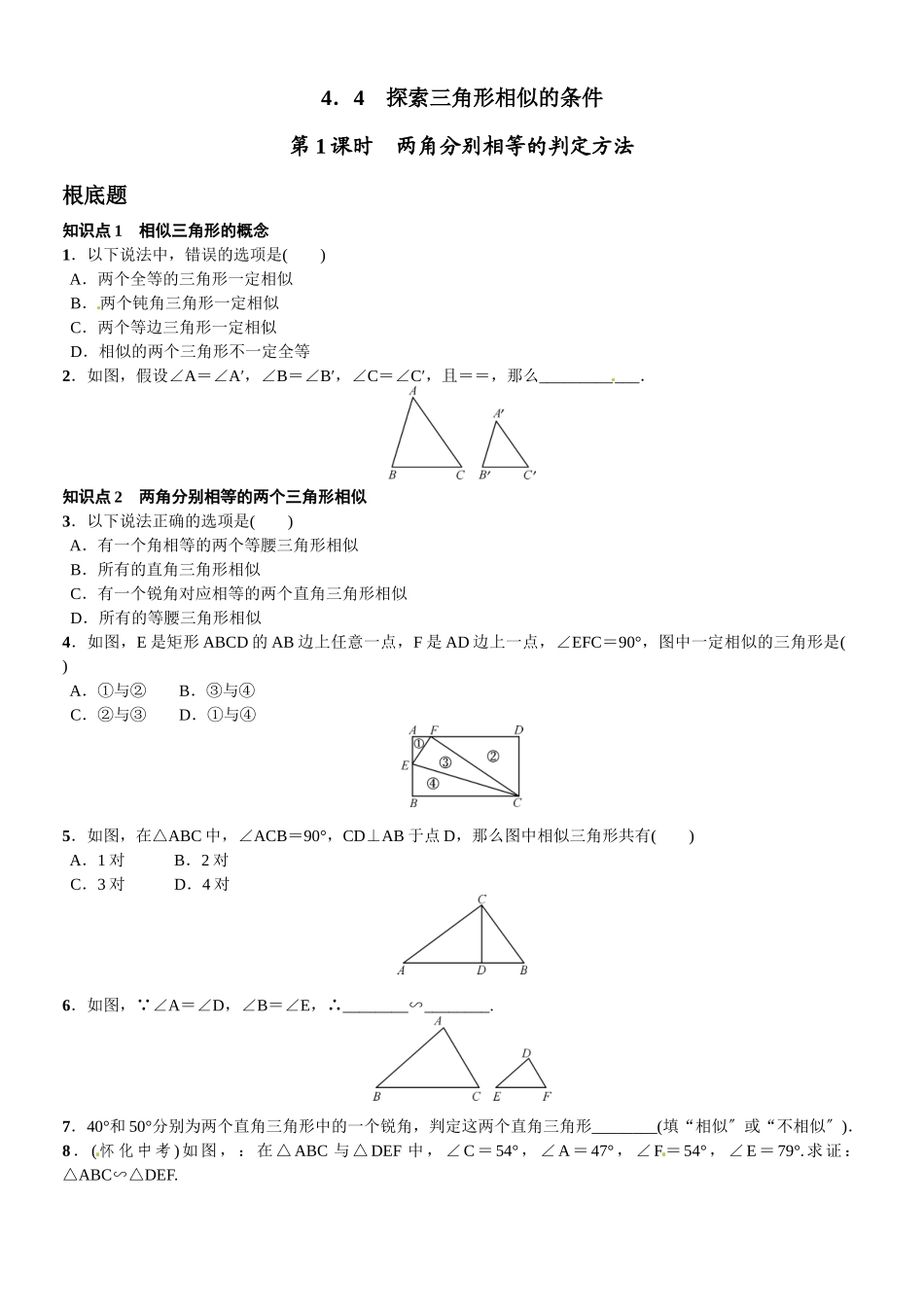
4.4探索三角形相似的条件第1课时两角分别相等的判定方法根底题知识点1相似三角形的概念1.以下说法中,错误的选项是()A.两个全等的三角形一定相似B.两个钝角三角形一定相似C.两个等边三角形一定相似D.相似的两个三角形不一定全等2.如图,假设∠A=∠A′,∠B=∠B′,∠C=∠C′,且==,那么____________.知识点2两角分别相等的两个三角形相似3.以下说法正确的选项是()A.有一个角相等的两个等腰三角形相似B.所有的直角三角形相似C.有一个锐角对应相等的两个直角三角形相似D.所有的等腰三角形相似4.如图,E是矩形ABCD的AB边上任意一点,F是AD边上一点,∠EFC=90°,图中一定相似的三角形是()A.①与②B.③与④C.②与③D.①与④5.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,那么图中相似三角形共有()A.1对B.2对C.3对D.4对6.如图, ∠A=∠D,∠B=∠E,∴________∽________.7.40°和50°分别为两个直角三角形中的一个锐角,判定这两个直角三角形________(填“相似〞或“不相似〞).8.(怀化中考)如图,:在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证:△ABC∽△DEF.[来源:学_科_网Z_X_X_K][来源:Z。xx。k.Com]9.(铜仁中考)如以下图,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.[来源:Z+xx+k.Com]中档题10.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么以下判断中,错误的选项是()A.△ADE∽△ABCB.△ADE∽△ACDC.△DEC∽△CDBD.△ADE∽△DCB11.(海南中考)如图,点P是□ABCD边AB上的一点,射线CP交DA的延长线于点E,那么图中相似的三角形有()A.0对B.1对C.2对D.3对12.在△ABC中,∠C=90°,D是边AB上一点(不与点A,B重合),过点D作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有()A.1条B.2条C.3条D.4条13.(毕节中考)如图,△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,那么DC的长等于()[来源:学科网ZXXK]A.B.C.D.14.如图,△ABC、△DEP是两个全等的等腰直角三角形,∠BAC=∠PDE=90°.(1)假设将△DEP的顶点P放在BC上(如图1),PD、PE分别与AC、AB相交于点F、G.求证:△PBG∽△FCP;(2)假设使△DEP的顶点P与顶点A重合(如图2),PD、PE与BC相交于点F、G.试问△PBG与△FCP还相似吗?为什么?综合题15.在△ABC中,∠C=90°.(1)如图1,P是AC上的点,过点P作直线截△ABC,使截得的三角形与△ABC相似.例如:过点P作PD...