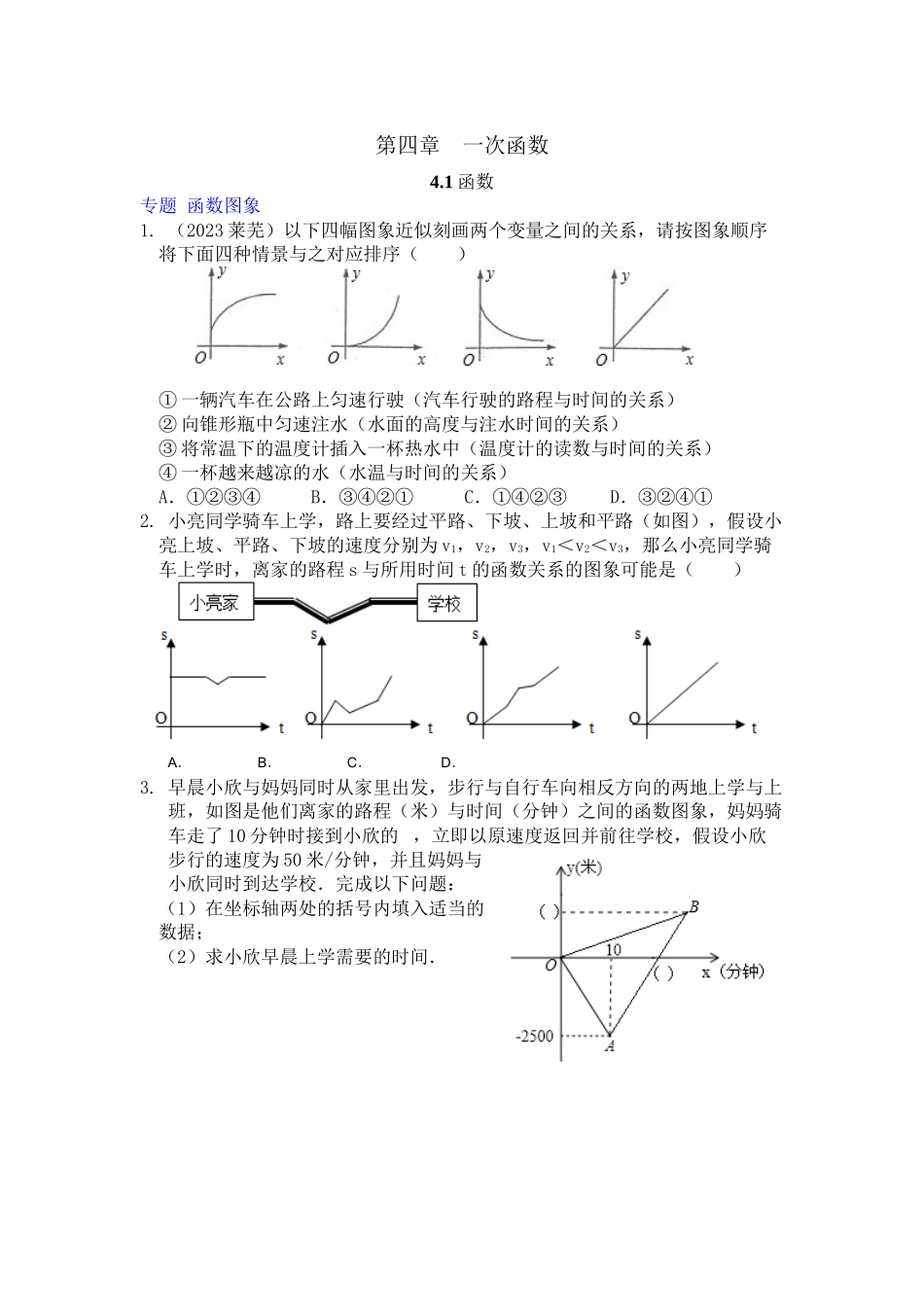
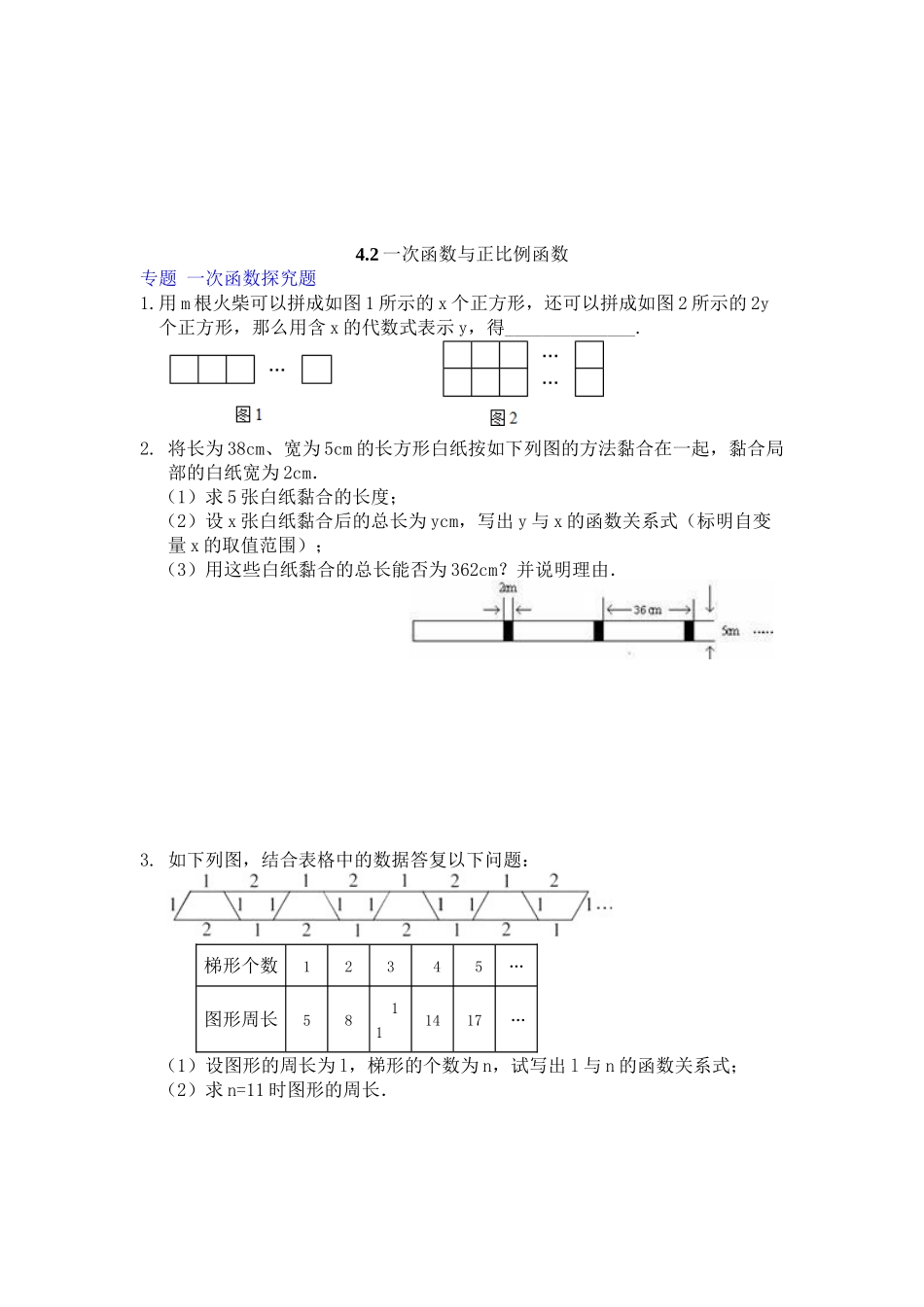
第四章一次函数4.1函数专题函数图象1.(2023莱芜)以下四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序()①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)②向锥形瓶中匀速注水(水面的高度与注水时间的关系)③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)④一杯越来越凉的水(水温与时间的关系)A.①②③④B.③④②①C.①④②③D.③②④①2.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),假设小亮上坡、平路、下坡的速度分别为v1,v2,v3,v1<v2<v3,那么小亮同学骑车上学时,离家的路程s与所用时间t的函数关系的图象可能是()A.B.C.D.3.早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程(米)与时间(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小欣的,立即以原速度返回并前往学校,假设小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成以下问题:(1)在坐标轴两处的括号内填入适当的数据;(2)求小欣早晨上学需要的时间.答案:www.1.D【解析】③将常温下的温度计插入一杯热水中温度计的读数一开始较快,后来变慢;②向锥形瓶中匀速注水,水面的高度一开始随注水时间的增加较慢,后来变快;④一杯越来越凉的水,水温随着时间的增加而越来越低;①一辆汽车在公路上匀速行驶,汽车行驶的路程与时间成正比例关系.故顺序为③②④①.应选D.2.C【解析】A.从图象上看小亮走平路的路程不变是不正确的;B.从图象上看小亮走的路程有一段随时间变少了,不正确;C.小亮走的路程应随时间的增大而增大,两次平路的两条直线互相平行,此图象符合,故正确;D.因为平路和上坡路及下坡路的速度不一样,所以不应是一条直线.应选C.3.解:(1)x轴处填20,y轴处填1250;(2)由图象可知,点A的坐标为(10,-2500),说明妈妈骑车速度为250米/分钟,并且返回到家的时间为20分钟,设小欣早晨上学需要的时间为x分钟,那么妈妈到家后在B处追到小欣的时间为(x-20)分钟,根据题意得:50x=250(x-20),解得x=25,答:小欣早晨上学需要的时间为25分钟.4.2一次函数与正比例函数专题一次函数探究题1.用m根火柴可以拼成如图1所示的x个正方形,还可以拼成如图2所示的2y个正方形,那么用含x的代数式表示y,得______________.2.将长为38cm、宽为5cm的长方形白纸按如下列图的方法黏合在一起,黏合局部的白纸宽为2...