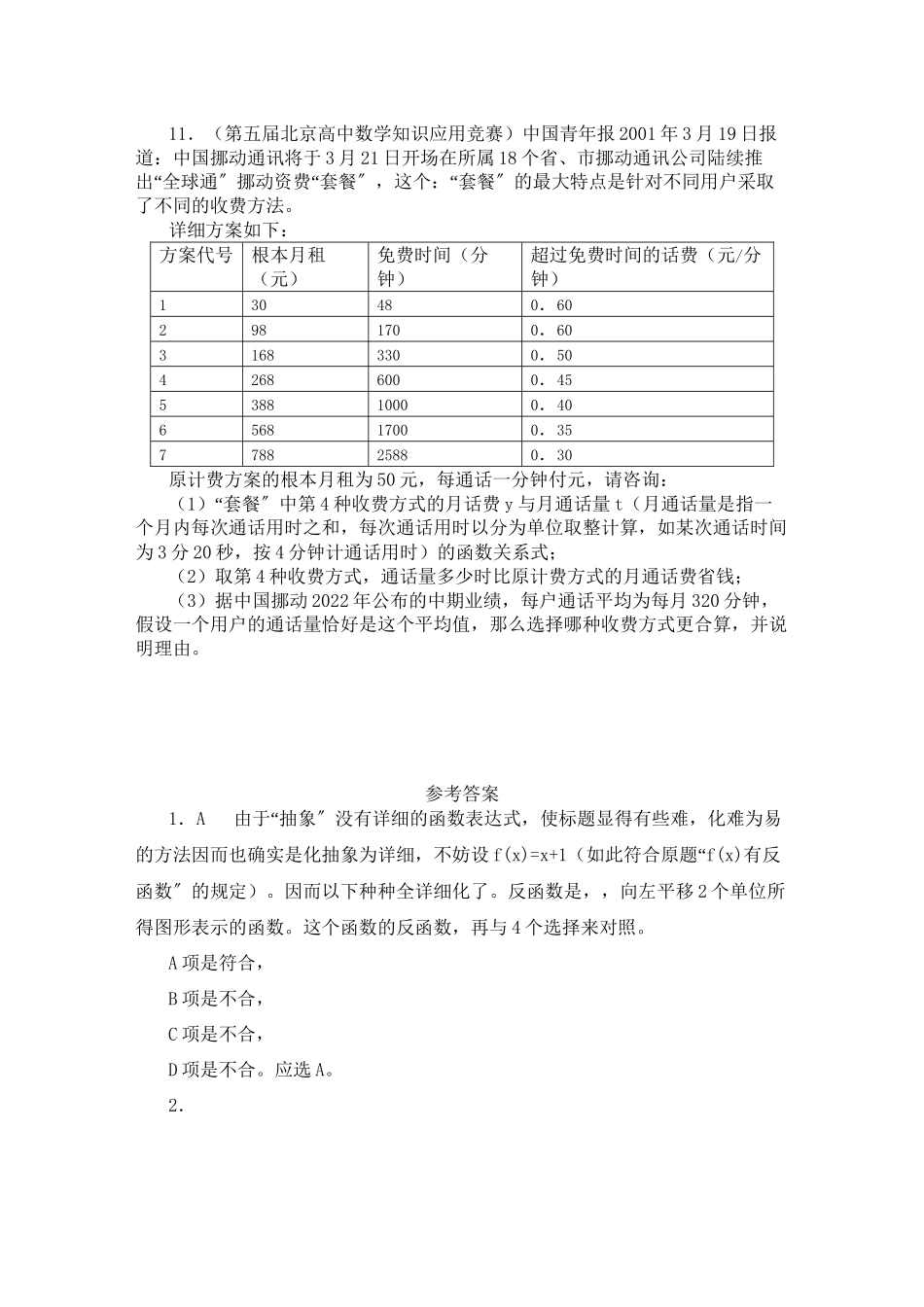
函数奥赛竞赛练习一、选择题1.(2022年北京市中学生数学竞赛)已经知道函数y=f(x)有反函数,现将y=f(2x-1)的图象向左平移2个单位,所得图形表示的函数的反函数是()A.B.C.D.二、填空题2.(2022年全国高中数学联赛)函数的值域为_____。3.(2022年全国高中数学联赛)不等式的解集为___________。4.(2022年北京市中学生数学竞赛)函数f(x)关于任意非负实数x、y都满足,且f(x)≥0,f(1)≠0,那么=______。三、解答题5.(2022年北京市中学生数学竞赛)f(x)是定义在R上的函数,对任意的x∈R,都有f(x+3)≤f(x)+3和f(x+2)≥f(x)+2,设g(x)=f(x)-x,(1)求证g(x)是周期函数;(2)假设f(998)=1002,求f(2022)的值。6.(2022年全国高中数学联赛)假设函数在区间[a,b]上的最小值为2a,最大值为2b,求区间[a,b]。7“.(第一届希望杯〞全国邀请赛试题)求函数在区间[-1,1]上的值域。8“.(第九届希望杯〞全国邀请赛试题)假设实数x满足不等式。试求函数的最大值。9.(2022年莫斯科师范大学数学奥林匹克竞赛)作函数的图象。10.(2022年莫斯科师范大学数学奥林匹克竞赛)函数是偶函数依然奇函数?11.(第五届北京高中数学知识应用竞赛)中国青年报2001年3月19日报道:中国挪动通讯将于3月21日开场在所属18个省、市挪动通讯公司陆续推“““出全球通〞挪动资费套餐〞,这个:套餐〞的最大特点是针对不同用户采取了不同的收费方法。详细方案如下:方案代号根本月租(元)免费时间(分钟)超过免费时间的话费(元/分钟)130480.602981700.6031683300.5042686000.45538810000.40656817000.35778825880.30原计费方案的根本月租为50元,每通话一分钟付元,请咨询:(1“)套餐〞中第4种收费方式的月话费y与月通话量t(月通话量是指一个月内每次通话用时之和,每次通话用时以分为单位取整计算,如某次通话时间为3分20秒,按4分钟计通话用时)的函数关系式;(2)取第4种收费方式,通话量多少时比原计费方式的月通话费省钱;(3)据中国挪动2022年公布的中期业绩,每户通话平均为每月320分钟,假设一个用户的通话量恰好是这个平均值,那么选择哪种收费方式更合算,并说明理由。参考答案1.A“由于抽象〞没有详细的函数表达式,使标题显得有些难,化难为易的方法因而也确实是化抽象为详细,不妨设f(x)=x+1“(如此符合原题f(x)有反函数〞的规定)。因而以下种种全详细化了。反函数是,,向左平移2个单位所得图形表示的函数。这个函数的反函...