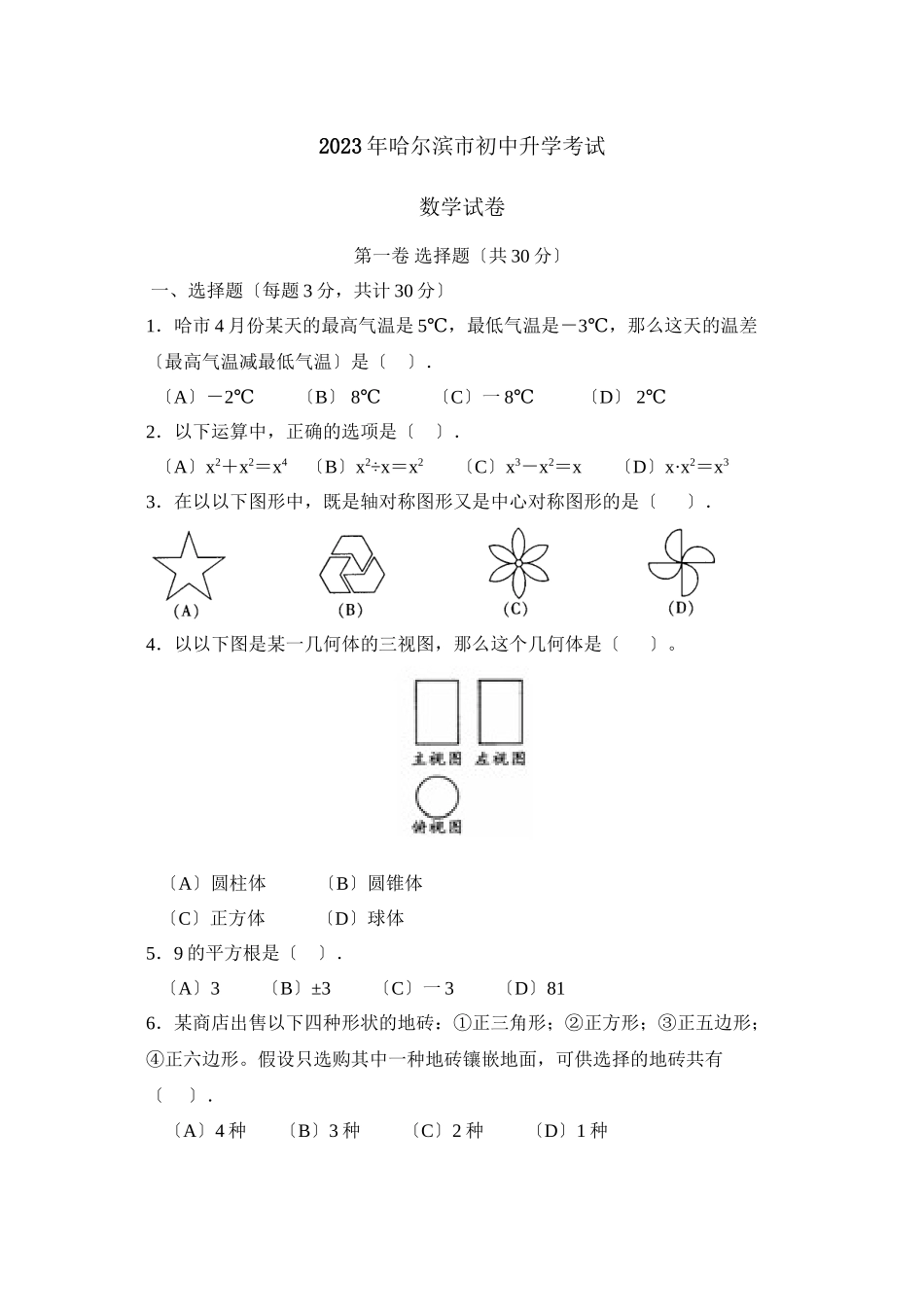
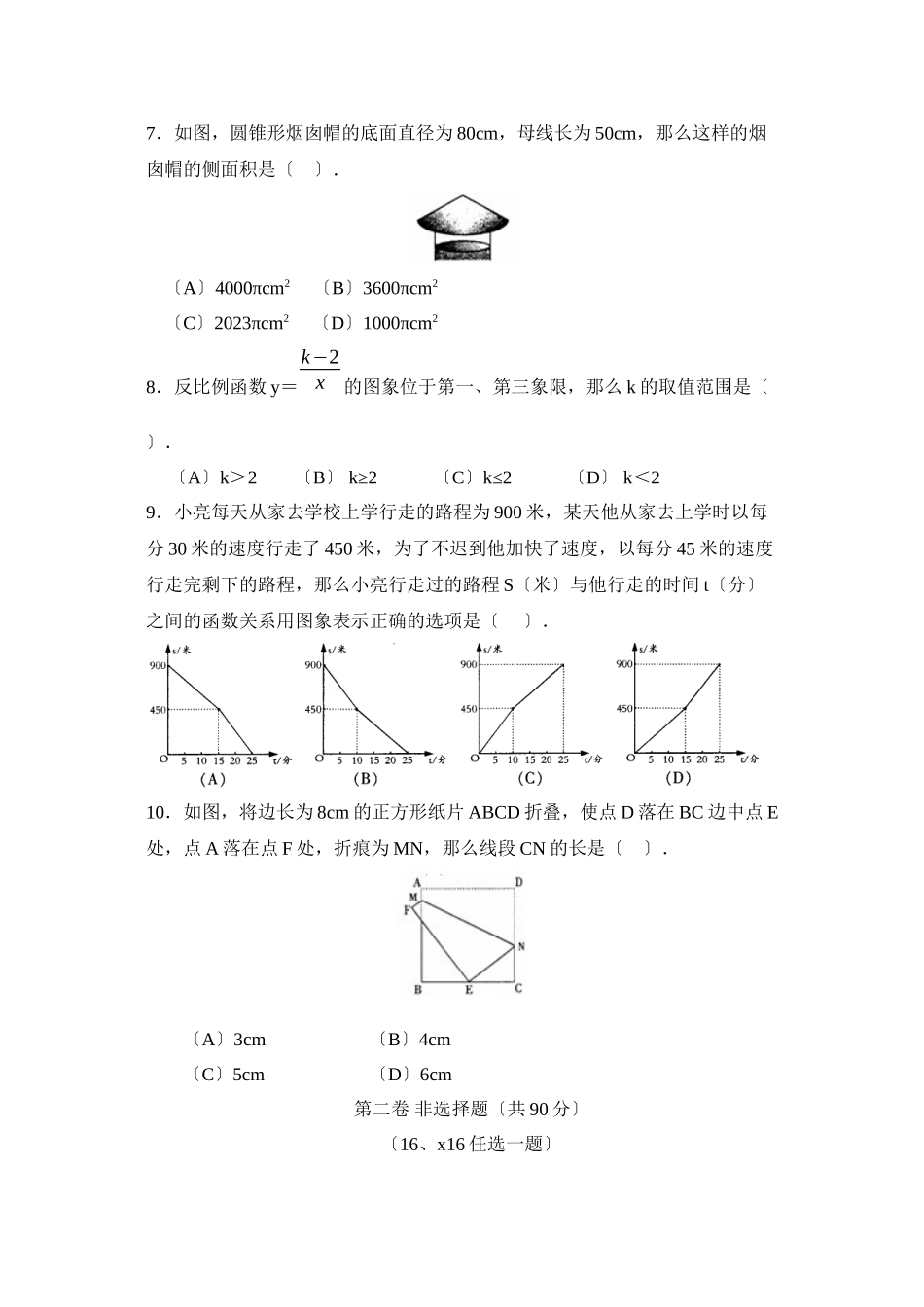
2023年哈尔滨市初中升学考试数学试卷第一卷选择题〔共30分〕一、选择题〔每题3分,共计30分〕1.哈市4月份某天的最高气温是5℃,最低气温是-3℃,那么这天的温差〔最高气温减最低气温〕是〔〕.〔A〕-2℃〔B〕8℃〔C〕一8℃〔D〕2℃2.以下运算中,正确的选项是〔〕.〔A〕x2+x2=x4〔B〕x2÷x=x2〔C〕x3-x2=x〔D〕x·x2=x33.在以以下图形中,既是轴对称图形又是中心对称图形的是〔〕.4.以以下图是某一几何体的三视图,那么这个几何体是〔〕。〔A〕圆柱体〔B〕圆锥体〔C〕正方体〔D〕球体5.9的平方根是〔〕.〔A〕3〔B〕±3〔C〕一3〔D〕816.某商店出售以下四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形。假设只选购其中一种地砖镶嵌地面,可供选择的地砖共有〔〕.〔A〕4种〔B〕3种〔C〕2种〔D〕1种7.如图,圆锥形烟囱帽的底面直径为80cm,母线长为50cm,那么这样的烟囱帽的侧面积是〔〕.〔A〕4000πcm2〔B〕3600πcm2〔C〕2023πcm2〔D〕1000πcm28.反比例函数y=k−2x的图象位于第一、第三象限,那么k的取值范围是〔〕.〔A〕k>2〔B〕k≥2〔C〕k≤2〔D〕k<29.小亮每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分30米的速度行走了450米,为了不迟到他加快了速度,以每分45米的速度行走完剩下的路程,那么小亮行走过的路程S〔米〕与他行走的时间t〔分〕之间的函数关系用图象表示正确的选项是〔〕.10.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,那么线段CN的长是〔〕.〔A〕3cm〔B〕4cm〔C〕5cm〔D〕6cm第二卷非选择题〔共90分〕〔16、x16任选一题〕二、填空题〔每题3分,共计24分〕11.太阳的半径约是69660千米,用科学记数法表示〔保存3个有效数字〕约是千米.12.函数y=xx−1的自变量x的取值范围是.13.把多项式2mx2-4mxy+2my2分解因式的结果是.14.如图,AB为⊙O的弦,⊙O的半径为5,OCAB⊥于点D,交⊙O于点C,且CD=l,那么弦AB的长是.15.一个袋子中装有6个球,其中4个黑球2个白球,这些球除颜色外,形状、大小、质地等完全相同.搅匀后,在看不到球的条件下,随机从这个袋子中摸出一个球为白球的概率是.16.2008年7月1日是星期二,那么2008年7月16日是星期.x16.假设x=1是一元二次方程x2+x+c=0的一个解,那么c2=.17.观察以以下图形:它们是按一定规律排列的,依照此规律,第20个图形共有个★.18.菱形ABCD的边长是6,点E...