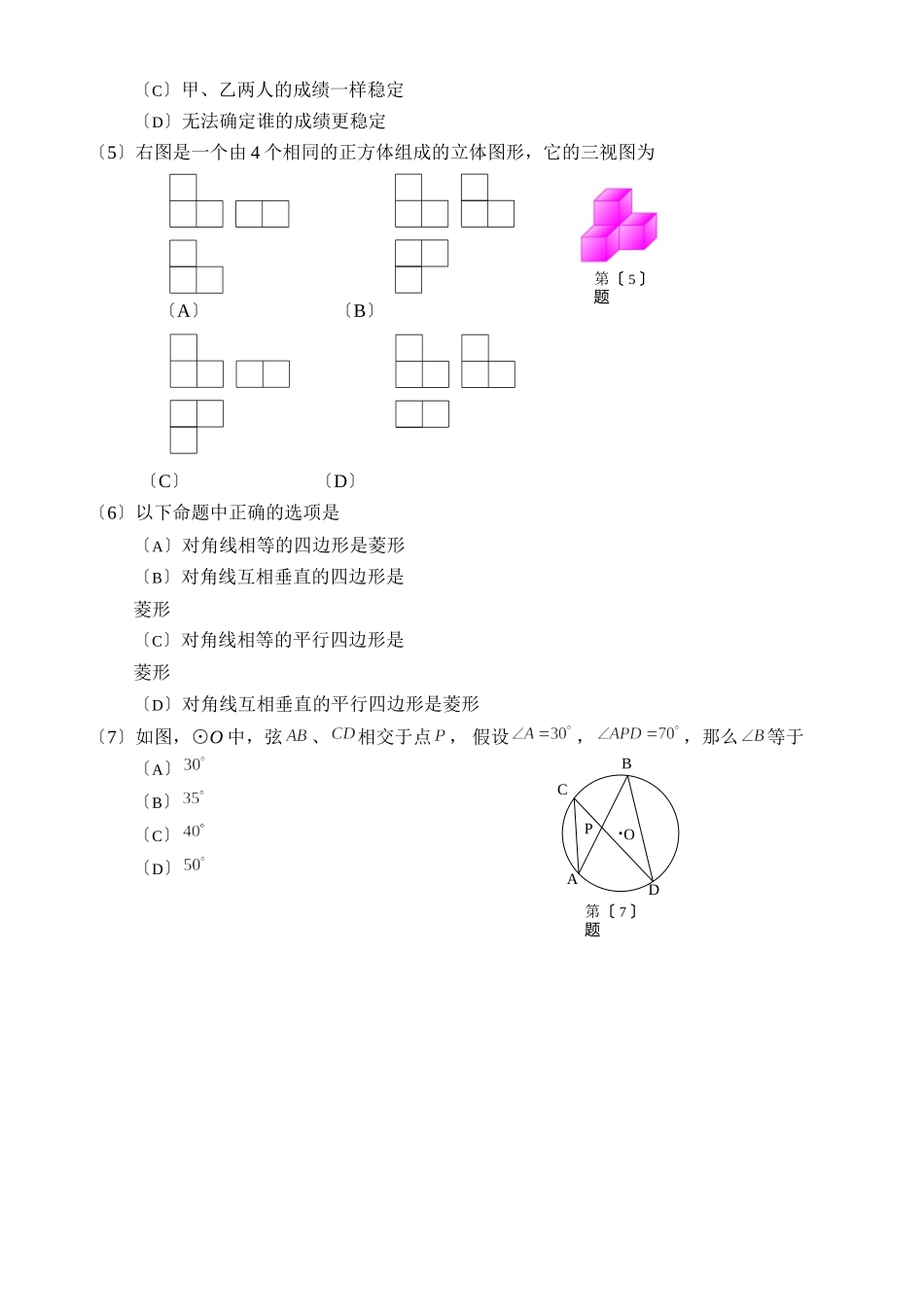
2023年天津市初中毕业生学业考试试卷数学本试卷分为第一卷〔选择题〕、第二卷〔非选择题〕两局部。第一卷第1页至第3页,第二卷第4页至第8页。试卷总分值120分。考试时间100分钟。“答卷前,考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在答题卡〞“上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在答题卡〞上,答案答在试卷上无效“。考试结束后,将本试卷和答题卡〞一并交回。祝各位考生考试顺利!第一卷〔选择题共30分〕本卷须知:每题选出答案后,用2B“铅笔把答题卡〞上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。一、选择题:本大题共10小题,每题3分,共30分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.〔1〕的值等于〔A〕〔B〕〔C〕〔D〕1〔2〕以以下图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为〔A〕〔B〕〔C〕〔D〕〔3〕上海世博会是我国第一次举办的综合类世界博览会.据统计自2010年5月1日开幕至5月31日,累计参观人数约为8030000人,将8030000用科学记数法表示应为〔A〕〔B〕〔C〕〔D〕〔4〕在一次射击比赛中,甲、乙两名运发动10次射击的平均成绩都是7环,其中甲的成绩的方差为1.21,乙的成绩的方差为3.98,由此可知〔A〕甲比乙的成绩稳定〔B〕乙比甲的成绩稳定〔C〕甲、乙两人的成绩一样稳定〔D〕无法确定谁的成绩更稳定〔5〕右图是一个由4个相同的正方体组成的立体图形,它的三视图为〔A〕〔B〕〔C〕〔D〕〔6〕以下命题中正确的选项是〔A〕对角线相等的四边形是菱形〔B〕对角线互相垂直的四边形是菱形〔C〕对角线相等的平行四边形是菱形〔D〕对角线互相垂直的平行四边形是菱形〔7〕如图,⊙O中,弦、相交于点,假设,,那么等于〔A〕〔B〕〔C〕〔D〕第〔5〕题第〔7〕题BCADPO〔8〕比拟2,,的大小,正确的选项是〔A〕〔B〕〔C〕〔D〕〔9——“〕如图,是一种古代计时器漏壶〞的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.假设用表示时间,表示壶底到水面的高度,下面的图象适合表示一小段时间内与的函数关系的是〔不考虑水量变化对压力的影响〕〔A〕〔B〕〔C〕〔D〕〔10〕二次函数()的图象如以下图,有以下结论:①;②;③;④.其中,正确结论的个数是〔A〕1〔B〕2〔C〕3〔D〕4x第〔9〕题yOxyOxyOxyO第〔10〕题yxO1x122023年天津市初中毕业生学业考试试...