b3b442d0-643d-11eb-80a9-e70120345ba62022考研数学零基础提前学作业4（答案）考研资料.pdf

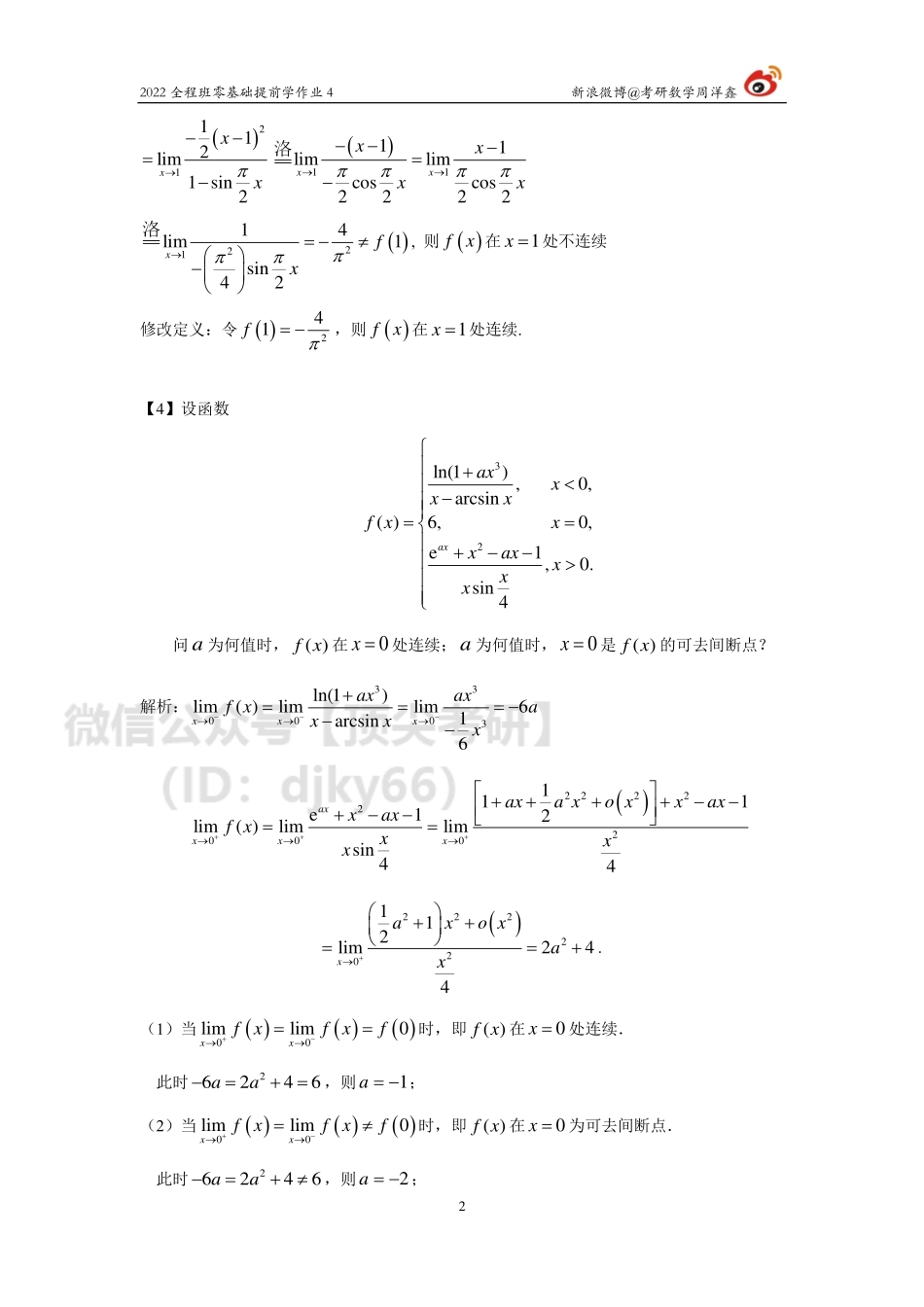
2022 全程班零基础提前学作业 4 新浪微博考研数学周洋鑫 1 2022 年一笑而过全程班“提前学”课程作业 同步作业 4 考点 3 函数连续与间断【1】若函数1cos,0(),0 xxf xaxbx=在0 x=处连续，则（A）12ab=（B）12ab=（C）0ab=（D）2ab=解析：因为()f x在0 x=连续，所以00lim()lim()(0)xxf xf xf+=;由 20001()1 cos12lim()limlim,2xxxxxf xaxaxa+=0lim()(0)xf xfb=；得12ba=，即12ab=故选（A）【2】若2sin21,0(),0axxexf xxa x+=，在(,)+上连续，则a=.解析：由初等函数在其定义区间内必连续可知，()fx在0 x 时必连续，因此仅需讨论0 x=处连续，即()()0lim0 xf xf=.()220000sin21sin21limlimlimlimaxaxxxxxxexef xxxx+=+22aa=+=则2a=.【3】设函数lncos(1),1,1 sin()21,1.xxxf xx=问函数()f x在1x=处是否连续?若不连续,修改函数在1x=处的定义使之连续.解析：()()()111lncos1cos11limlimlim1 sin1 sin22xxxxxf xxx=2022 全程班零基础提前学作业 4 新浪微博考研数学周洋鑫 2 ()21112lim1 sin2xxx=()1111limlimcoscos2222xxxxxx=洛()22114lim1sin42xfx=洛,则()fx在1x=处不连续 修改定义：令()241f=，则()fx在1x=处连续.【4】设函数 32ln(1),0,arcsin()6,0,e1,0.sin4axaxxxxf xxxaxxxx+=+问a为何值时，()f x在0 x=处连续；a为何值时，0 x=是()f x的可去间断点？解析：330003ln(1)lim()limlim61arcsin6xxxaxaxf xaxxx+=()222222000111e12lim()limlimsin44axxxxaxa xo xxaxxaxf xxxx+=()222220112lim244xaxo xax+=+.（1）当()()()00limlim0 xxf xf xf+=时，即()f x在0 x=处连续 此时26246aa=+=，则1=a；（2）当()()()00limlim0 xxf xf xf+=时，即()f x在0 x=为可去间断点 此时26246aa=+，则2=a；2022 全程班零基础提前学作业 4 新浪微博考研数学周洋鑫 3 考点 4 导数定义（1）【1】设()(1)(2)()f xx xxxn=+，则(0)f=_.解析：()()()()()00010limlim0 xxf xfx xxnfxx+=()()()0lim12!xxxxnn=+=【2】设函数()f x在0 x=处可导,(0)0,(0)ffb=,若函数()sin,0,(),0.f xaxxF xxAx+=在0 x=处连续,则常数A=_.解析：由于()F x在0 x=处连续，则()()0F xFA=故：()()()()0000sin0sinlimlimlimlimxxxxf xaxf xfaxF xxxx+=+()0fabaAab=+=+=+【3】设()221sin,0,11 cos,0,xxxfxxxx+=则()fx在0 x=处（）.（A）极限不存在.（B）极限存在但不连续.（C）连续但不可导.（D）可导.解析：()22001limlimsin01xxf xxx=+()200011 cos2limlimlim0 xxxxxf xxx+=则：()()0lim00 xf xf=在0 x=处极限存在且连续.()222001sin110limlimsin01xxxxfxxx+=+2022 全程班零基础提前学作业 4 新浪微博考研数学周洋鑫 4 ()200231 cos120limlim0 xxxxxfxx+=则：()()000ff+=在0 x=处可导 【4】设()f x在xa=的某个领域内有定义，则()f x在xa=处可导的一个充分条件是（A）1lim ()()hh f af ah+存在（B）0(2)()limhf ahf ahh+存在（C）0()()lim2hf ahf ahh+存在（D）0()()limhf af ahh存在 解析:利用导数的概念判定()f x在xa=处可导的充分条件，（A）只能保证函数在xa=右导数存在，故排除；（B）、（C）中0(2)()limhf ahf ahh+，0()()lim2hf ahf ahh+存在，并看不出xa=的关系，即使函数在xa=处不连续，其极限也有可能存在，所以（B）、（C）是()f x在xa=处可导的必要条件，而非充分条件。（D）中有，00()()()()limlimxhxhf axf af af ahxh=+=存在，显然是导数存在的充分条件,故选（D）.【5】已知函数()f x在0 x=处可导，且(0)0f=，则2330()2()limxx f xf xx=（A）2(0)f.（B）(0)f.（C）(0)f.（D）0.解析：()()22302limxx f xf xx()()()()()()3333000000lim2lim2lim0 xxxf xfxff xf xfxxxx+=()()()()3300000lim2lim0 xxfxff xfxx+=（*）（由于已知()0f 存在）2022 全程班零基础提前学作业 4 新浪微博考研数学周洋鑫 5 ()()()0200fff=选（B）【注】本题由已知()0f 存在，因此（*）可按四则运算拆开.