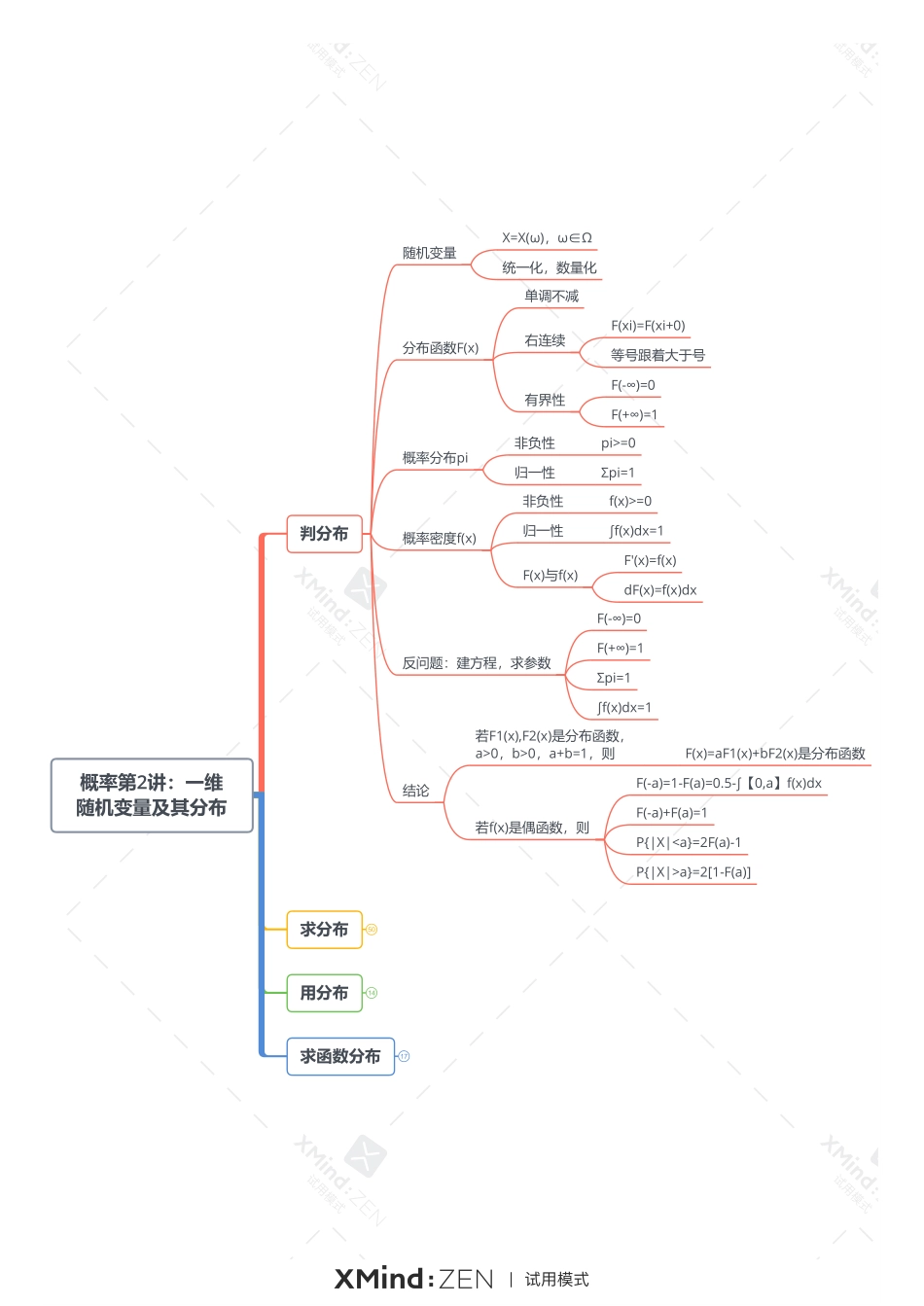
概率第2讲:一维随机变量及其分布判分布求分布50用分布14求函数分布17分布函数F(x)概率分布pi概率密度f(x)反问题:建方程,求参数随机变量统一化,数量化X=X(ω),ω∈Ω单调不减右连续有界性F(xi)=F(xi+0)F(-∞)=0F(+∞)=1等号跟着大于号F(-∞)=0F(+∞)=1Σpi=1∫f(x)dx=1非负性归一性pi>=0Σpi=1非负性f(x)>=0归一性∫f(x)dx=1F(x)与f(x)F'(x)=f(x)dF(x)=f(x)dx结论若F1(x),F2(x)是分布函数,a>0,b>0,a+b=1,则F(x)=aF1(x)+bF2(x)是分布函数若f(x)是偶函数,则F(-a)=1-F(a)=0.5-∫【0,a】f(x)dxF(-a)+F(a)=1P{|X|
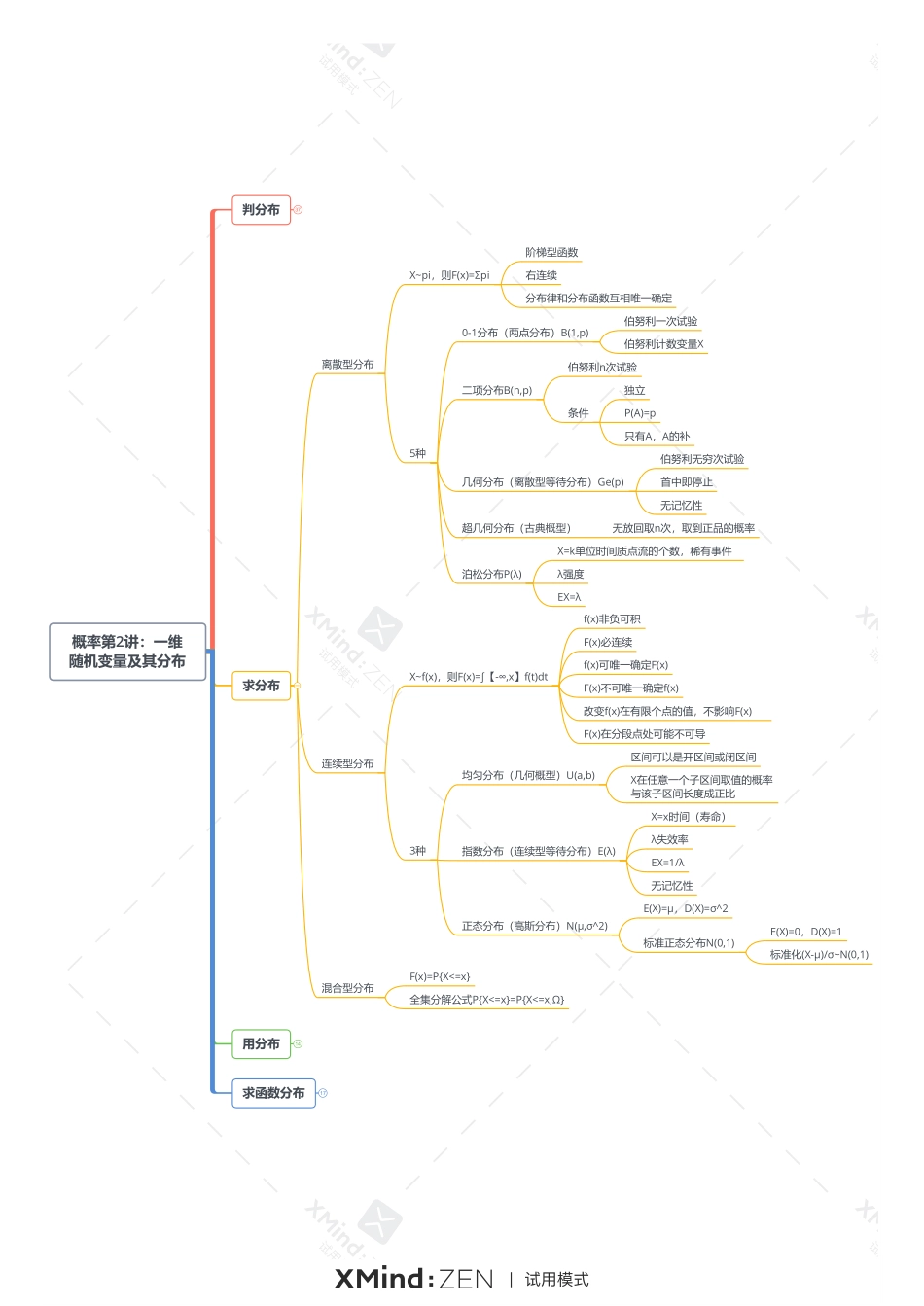
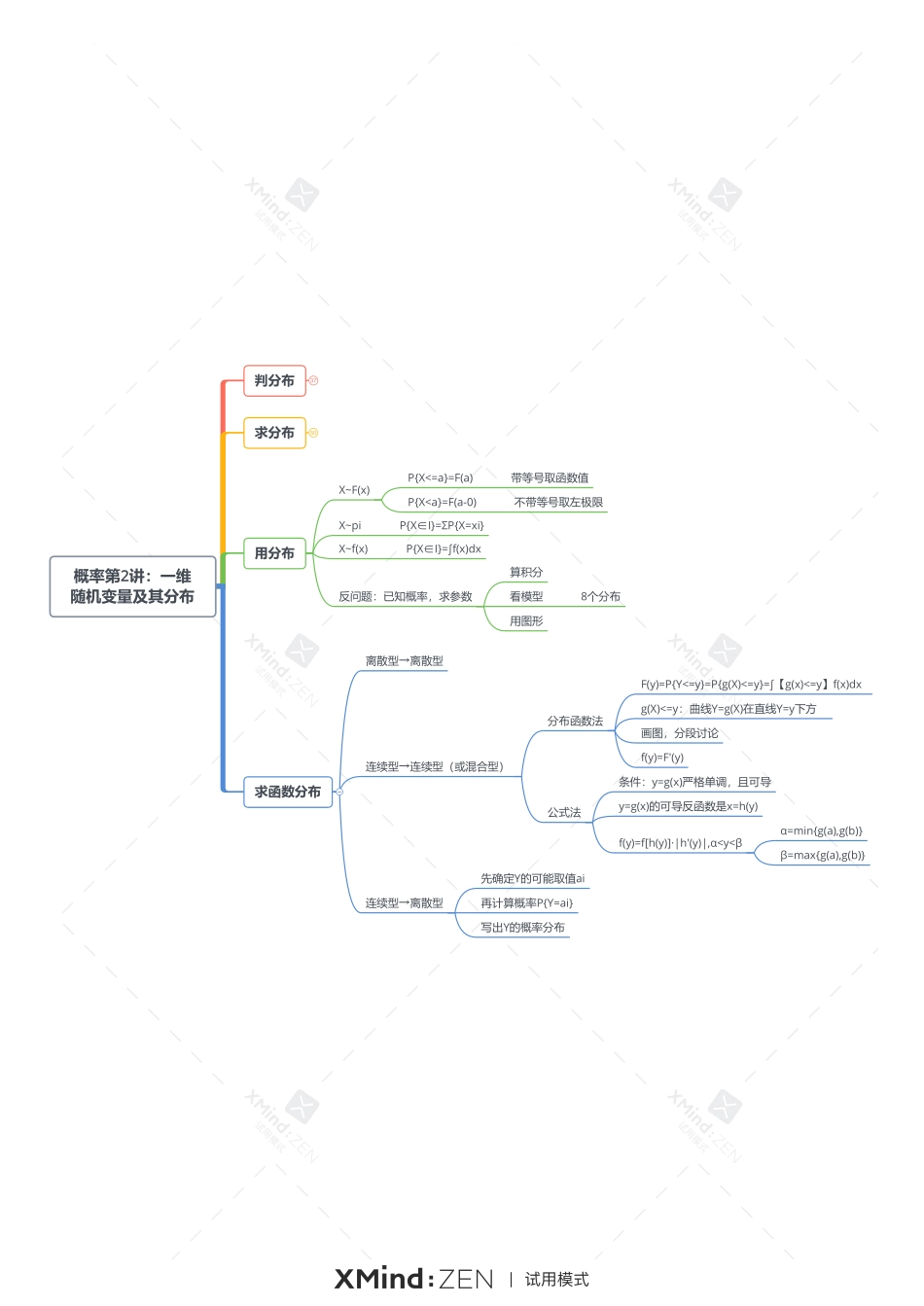
a}=2[1-F(a)]概率第2讲:一维随机变量及其分布判分布37求分布用分布14求函数分布17离散型分布连续型分布混合型分布X~pi,则F(x)=Σpi阶梯型函数右连续5种0-1分布(两点分布)B(1,p)二项分布B(n,p)几何分布(离散型等待分布)Ge(p)伯努利一次试验伯努利计数变量X伯努利n次试验条件独立P(A)=p只有A,A的补超几何分布(古典概型)伯努利无穷次试验首中即停止无放回取n次,取到正品的概率泊松分布P(λ)X=k单位时间质点流的个数,稀有事件λ强度EX=λX~f(x),则F(x)=∫【-∞,x】f(t)dtf(x)非负可积F(x)必连续3种分布律和分布函数互相唯一确定f(x)可唯一确定F(x)F(x)不可唯一确定f(x)改变f(x)在有限个点的值,不影响F(x)F(x)在分段点处可能不可导均匀分布(几何概型)U(a,b)指数分布(连续型等待分布)E(λ)正态分布(高斯分布)N(μ,σ^2)X=x时间(寿命)λ失效率EX=1/λ区间可以是开区间或闭区间X在任意一个子区间取值的概率与该子区间长度成正比无记忆性无记忆性E(X)=μ,D(X)=σ^2标准正态分布N(0,1)E(X)=0,D(X)=1标准化(X-μ)/σ~N(0,1)F(x)=P{X<=x}全集分解公式P{X<=x}=P{X<=x,Ω}概率第2讲:一维随机变量及其分布判分布37求分布50用分布求函数分布离散型→离散型连续型→连续型(或混合型)连续型→离散型X~F(x)X~piX~f(x)反问题:已知概率,求参数P{X<=a}=F(a)带等号取函数值P{X