S班线代强化第一章习题【公众号：小盆学长】免费分享.pdfVIP免费

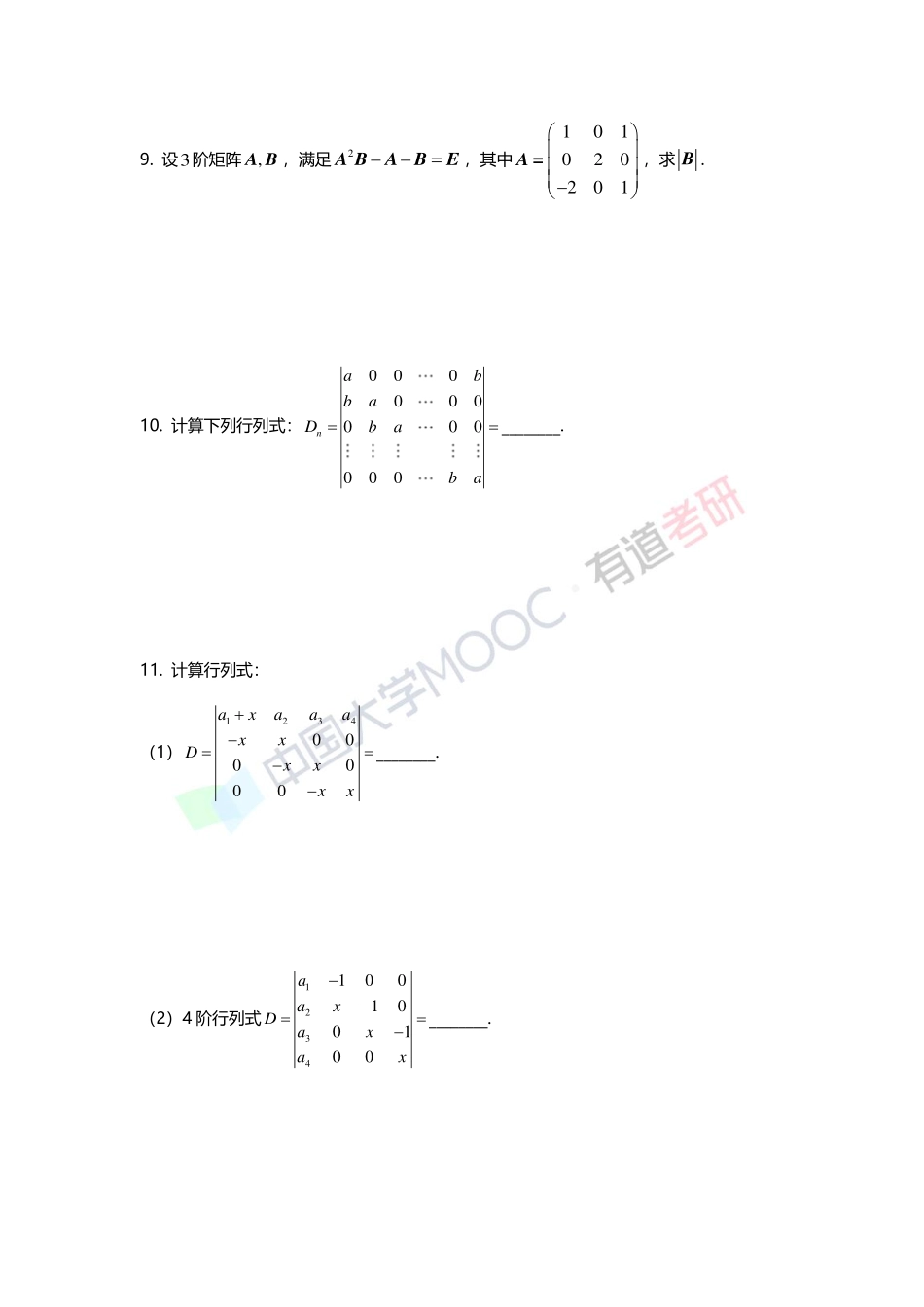
第一章行列式综合测试1.设2123211013xfxxxx，则2x的系数为________.2.设123,,,,为4维列向量，123,,,2Aαγγγ，123,,,93Bγγγ，求A+B.3.设113,,是三维线性无关的向量，A是三阶矩阵，且1122A，2234A，31232A，求A.4.设2512371459274612D，其中ijM是D中元素ija的余子式，则求21222324MMMM.5.设A为n阶矩阵，0aA的每行元素之和为b，则11211nAAA________.6.设12,为二维列向量，设12,A且4A，令12122,3B，则B________.7.5100011000110001100011aaaaDaaaaa________.8.计算0001000000001nababababDababab.9.设3阶矩阵,AB，满足2ABABE，其中101020201A=，求B.10.计算下列行列式：000000000000nabbaDbaba________.11.计算行列式：（1）1234000000axaaaxxDxxxx________.（2）4阶行列式1234100100100aaxDaxax________.（3）1111111111111111xxDxx________.12.设A是3阶可逆矩阵，1A的特征值为3,2,1，则A的代数余子式112233++AAA（A）16（B）13（C）12（D）1拓展提升1.设111213212223313233aaaaaaaaaA且210,a又2(,1,2,3)ijijAaij，则||A（A）2（B）4（C）6（D）82.（660）设100||020003A，ijA为(,)ij位置元素的代数余子式，则3,1ijijA________.3.已知A有0特征值，01111012002aaaabAB，且111220aaab，则011112aaa________.4.1221100001000001nnnnbbDbaaaaba________.5.（150）设12312,,,,均为四维列向量，1231(,,,)A，3122(,,,)B.若||1A，||2B，则|2|AB________.6.设123,,A，123,,为线性无关的3维列向量，P为3阶矩阵，123,2,3PA，则PE（A）6（B）6（C）24（D）247.已知3阶行列式||9A，其第2行元素为[1,1,2]，第3行元素为[2,2,1]，则3132333AAA________.8.设,AB为三阶矩阵，且~AB，121,2为A的两个特征值，||2B，求1*()(2)AEOOB.9.设A为3阶非零实矩阵，且T*kAA（k为非零常数）.（1）证明：A是可逆矩阵;（2）求行列式1*1|||()|.AA