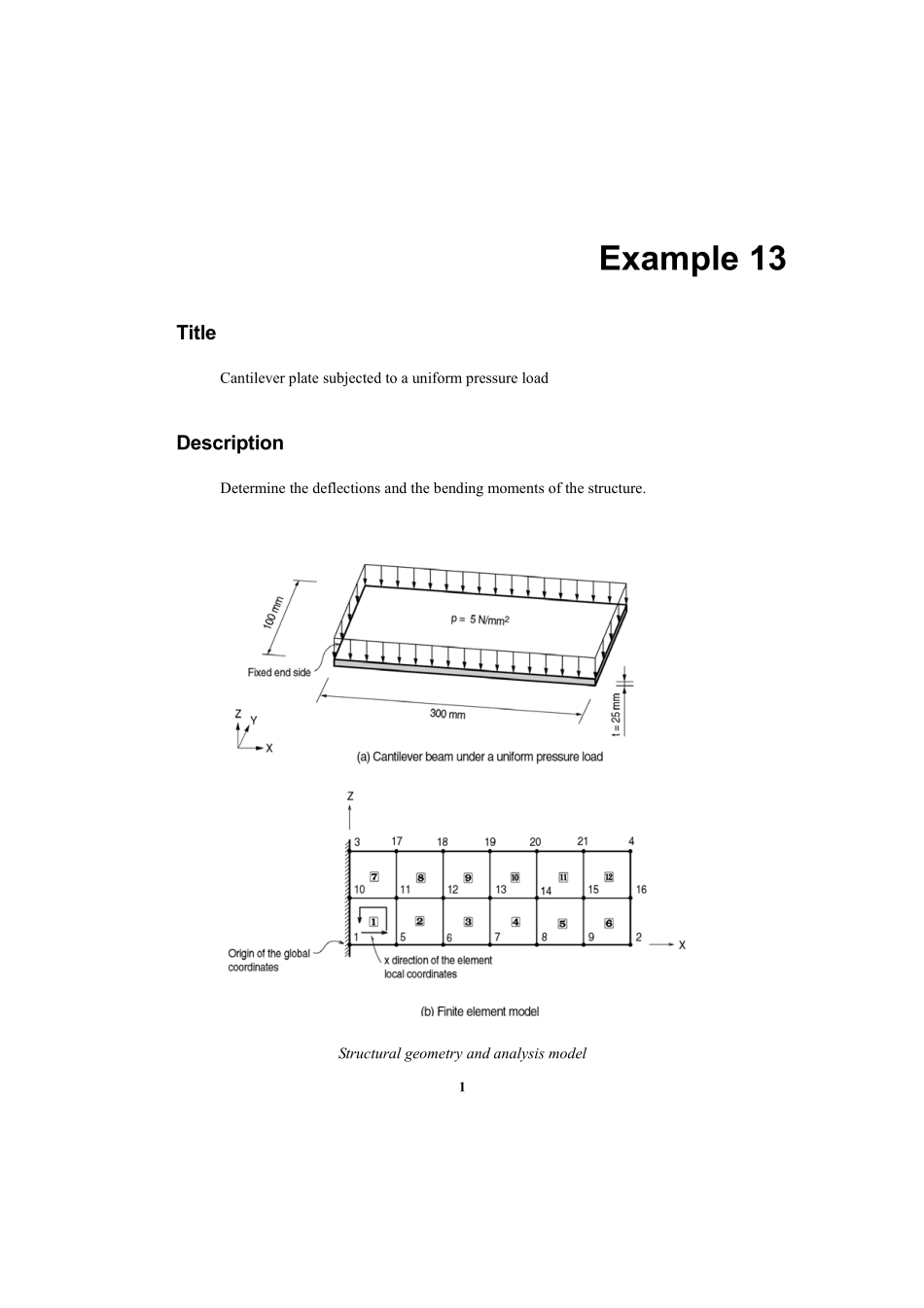
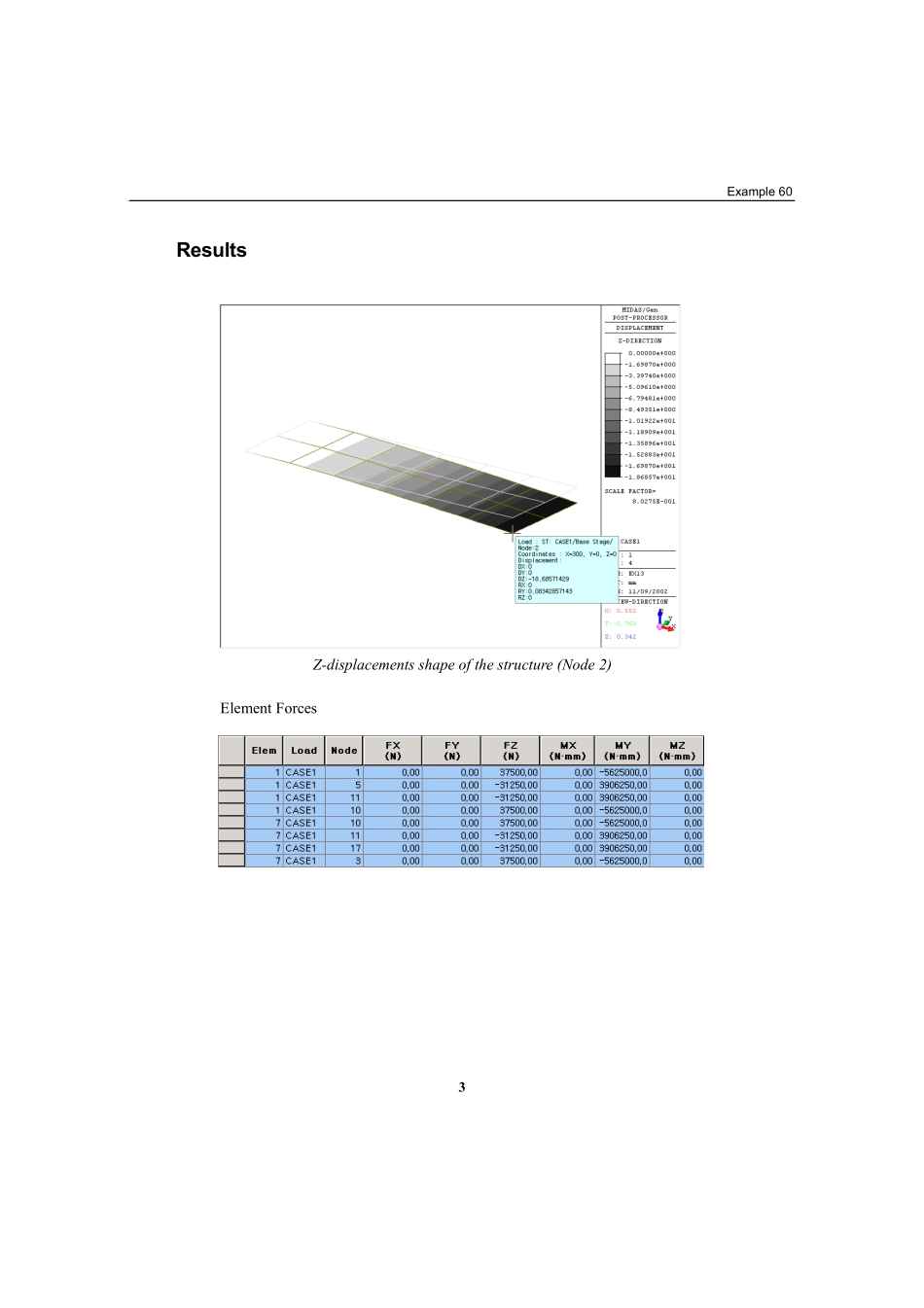
1Example13TitleCantileverplatesubjectedtoauniformpressureloadDescriptionDeterminethedeflectionsandthebendingmomentsofthestructure.Structuralgeometryandanalysismodel2ModelAnalysisType3-DstaticanalysisUnitSystemmm,NDimensionLength300mmWidth100mmThickness25mmElementPlateelement(Thicktype)MaterialModulusofelasticityE=2.1×105N/mm2ElementPropertySizea×b=50mm×50mmThicknesst=25mmBoundaryConditionNodes1,3and10;ConstrainallDOFs.LoadCaseAuniformpressureload,5N/mm2isdistributedovertheentirecantileverplateinthe-Zdirection.Example603ResultsZ-displacementsshapeofthestructure(Node2)ElementForces4ComparisonofResultsTheoreticalcalculationofthemaximumdeflectionandbendingmomentMaximumdeflection(δmax)=ElL82ω+GAsL22ω(atthefreeend)=)12/25100)(10210(8)300)(1005(334××××+)25100(6/51052)300)(1005(5/62×××××=8.51mmMaximumbendingmoment(Mmax)=ωL2/2(atthefixedend)=(5×100)(300)2/2=22.5×106N∙mmFEManalysisofthemaximumdeflectionandbendingmomentMaximumdeflection(δmax)=18.62mm(nodes2,16and4atthefreeend)Maximumbendingmoment(Mmax)=Numberofnodespertainingtothefixedendelements×thebendingmomentatonenode(nodes1&10oftheelement1andnodes3&10oftheelement7)=4×5625000N∙mm=22.5×106N∙mmUnit:mm,KNmResultTheoreticalSAP2000MIDAS/GenMaximumdeflection(δmax)18.61718.78818.686Maximumbendingmoment(Mmax)22.50×10622.50×10622.5×106ReferenceGere&Timoshenko,”MechanicsofMaterial”,1984