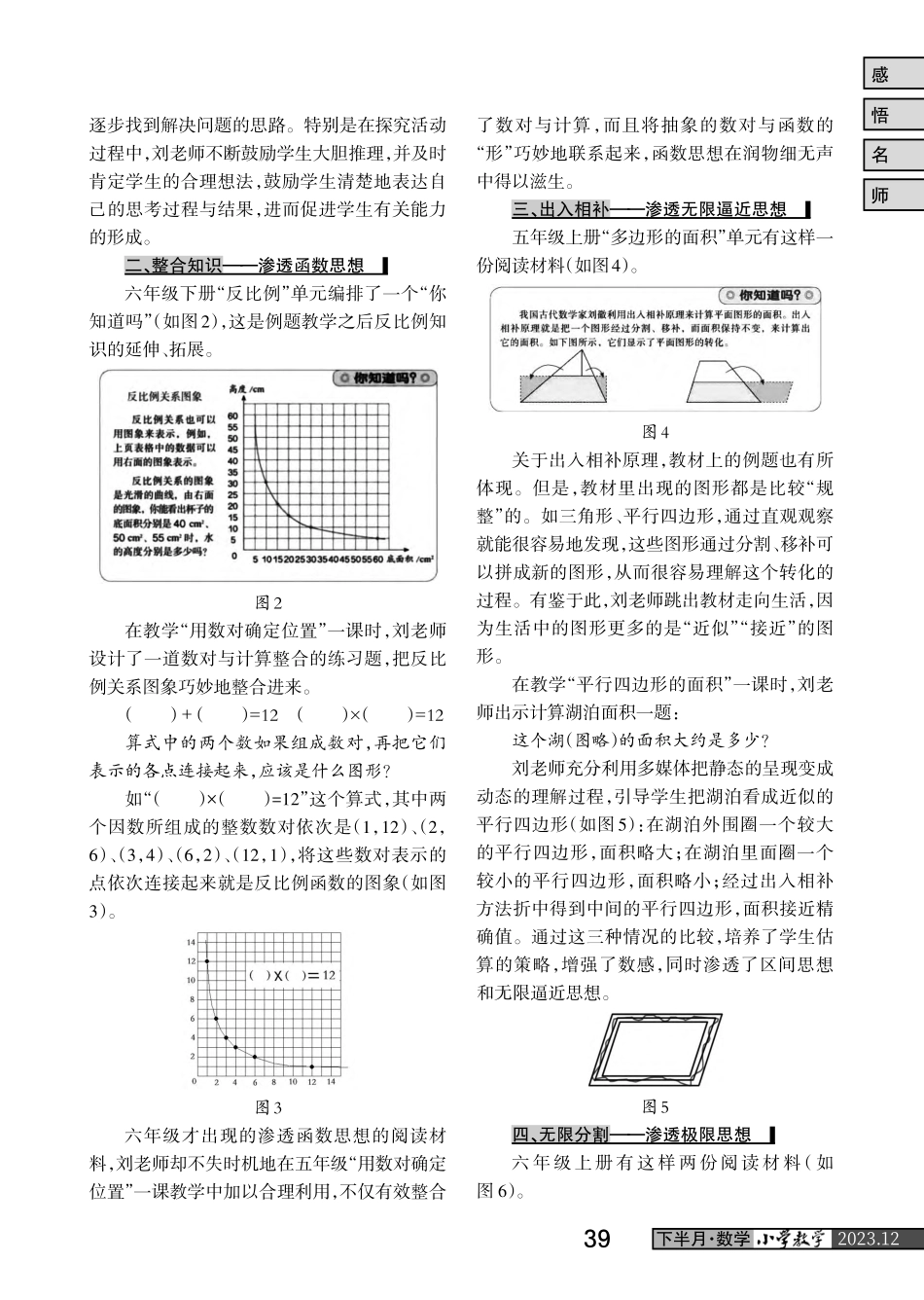
2023.12下半月·数学教材中编排的“你知道吗”阅读材料,主要介绍数学史、课外知识、拓展小知识等。这些似乎与考试无关的阅读材料,细细品读,其背后蕴含的数学思想以及介绍的数学文化,都是课内知识的延伸,对课内知识有很好的补充作用,可为学生打开思路、增长见识。“你知道吗”阅读材料,经过刘德武老师独具匠心的课堂演绎,成了学生分析、思考、探索问题的载体。下面选取刘老师课堂教学中的一些习题,以期“借题发挥”,从中找到刘老师充分发挥教材阅读材料作用的数学之“道”。一、“难”中求“易”——渗透化繁为简六年级下册(人教版教材,下同)有一份阅读材料——“斐波那契数列”(如图1),刘老师利用它设计了一节有高度、有深度的课,主要体现了“化难为易”的数学思想方法。(该阅读材料是2006年版教材六年级下册第65页的内容)图1首先看刘老师给出的阅读材料:斐波那契是中世纪数学家,他的研究对欧洲数学的发展有着深远的影响。他生于意大利的比萨,曾经到过东方和阿拉伯的许多地方。1202年,斐波那契出版了他的著作《算盘书》。在这部名著中,他率先将阿拉伯数字和十进制计数法介绍到欧洲,并提出了有趣的兔子问题。假定一对刚出生的小兔一个月后就能长成大兔,再过一个月便能生一对小兔,并且以后每个月都生一对小兔。一年内没有死亡。那么,由一对刚出生的兔子开始,12个月后会有多少对兔子呢?面对这个复杂的“兔子问题”,学生有些困惑,于是刘老师启发道:“这个问题有点儿复杂,面对一个困难的问题,怎么办呢?我向大家介绍一位中国古代非常有智慧的哲学家,道家的创始人——老子。他有这样一句名言——‘天下难事,必作于易’,也许对我们解决这个问题有所帮助。”在教学中,刘老师始终把握本课核心目标——数学思考。他引导学生从“天下难事,必作于易”入手找到解决问题的突破口,获得“柳暗花明又一村”的感受,并让学生从“易”中尝试解决问题,通过引导学生自主探究、独立思考,有意识地让学生体验由易到难、寻找规律,从而◇徐美义——刘德武老师有效利用阅读材料的启示感师悟名382023.12下半月·数学逐步找到解决问题的思路。特别是在探究活动过程中,刘老师不断鼓励学生大胆推理,并及时肯定学生的合理想法,鼓励学生清楚地表达自己的思考过程与结果,进而促进学生有关能力的形成。二、整合知识——渗透函数思想六年级下册“反比例”单元编排了一个“你知道吗”(如图2),这是例题教学之后反比例知识的延伸、拓展...