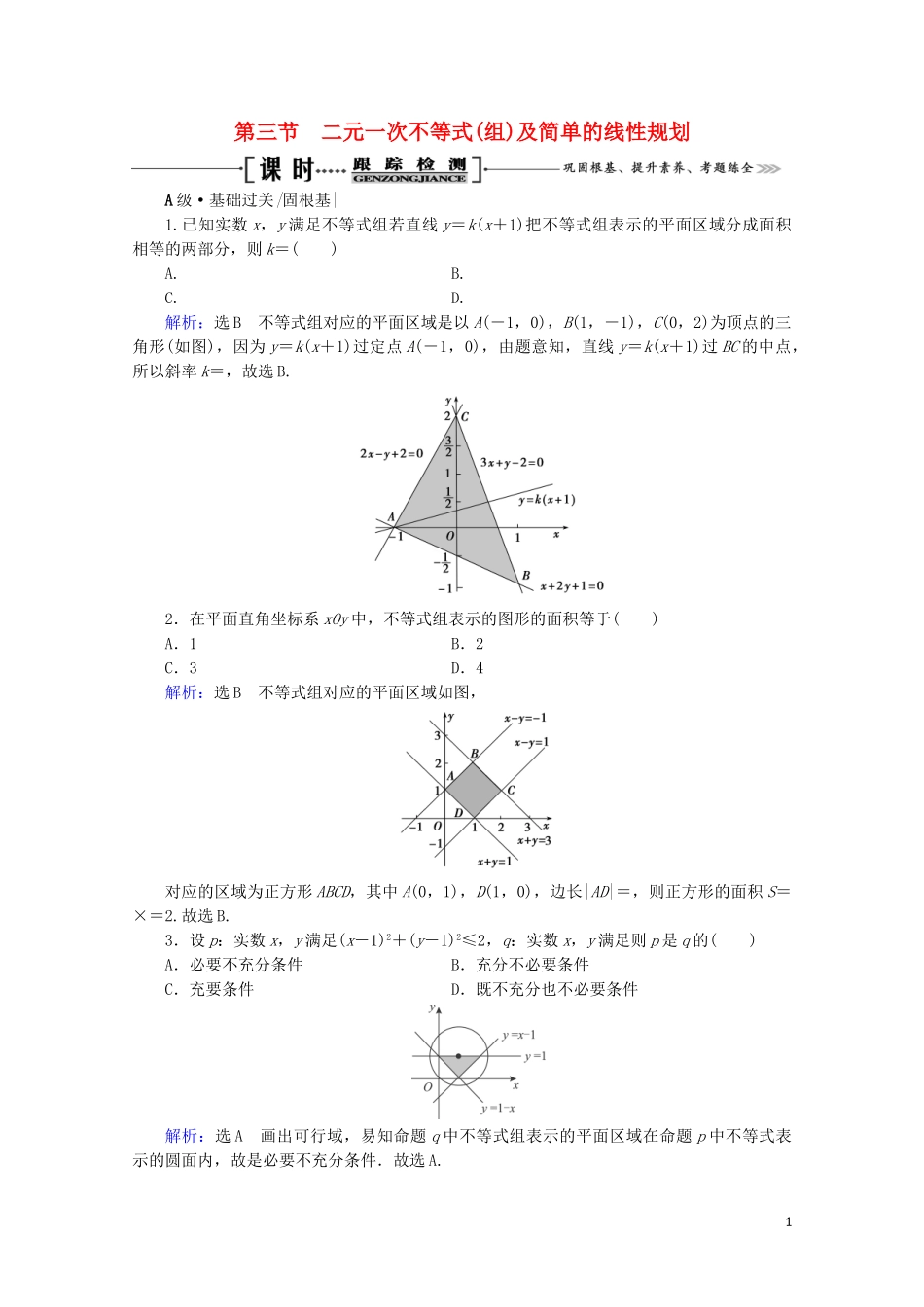
第三节二元一次不等式(组)及简单的线性规划A级·基础过关|固根基|1.已知实数x,y满足不等式组若直线y=k(x+1)把不等式组表示的平面区域分成面积相等的两部分,则k=()A.B.C.D.解析:选B不等式组对应的平面区域是以A(-1,0),B(1,-1),C(0,2)为顶点的三角形(如图),因为y=k(x+1)过定点A(-1,0),由题意知,直线y=k(x+1)过BC的中点,所以斜率k=,故选B.2.在平面直角坐标系xOy中,不等式组表示的图形的面积等于()A.1B.2C.3D.4解析:选B不等式组对应的平面区域如图,对应的区域为正方形ABCD,其中A(0,1),D(1,0),边长|AD|=,则正方形的面积S=×=2.故选B.3.设p:实数x,y满足(x-1)2+(y-1)2≤2,q:实数x,y满足则p是q的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要...