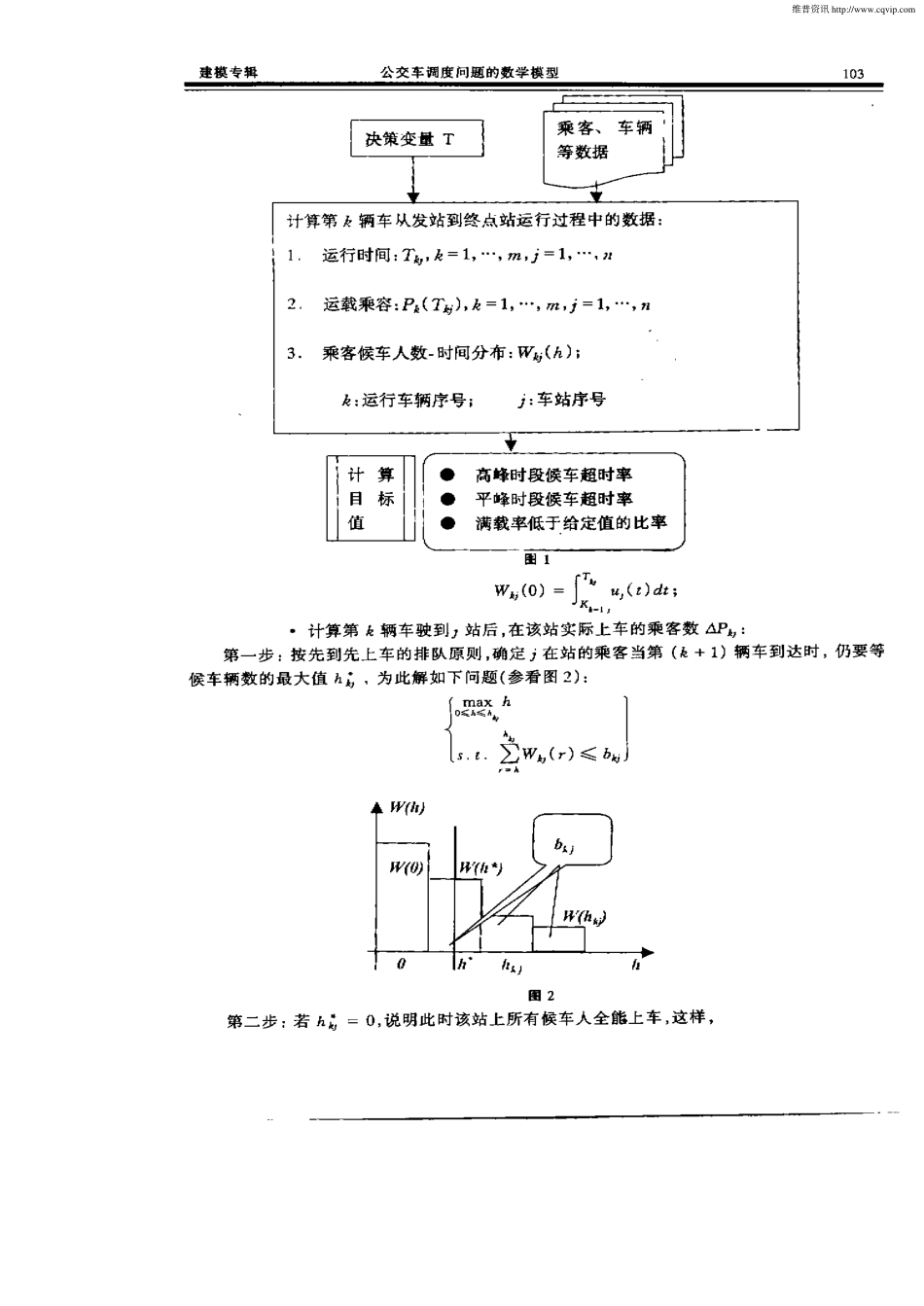
第19卷建模专辑工程数学学报v。【l9su口p。。。月JOURNALOFENGINEERINGMATHEMATICSFeb2002文章编号:10053085(2002)05—0101—06公交车调度问题的数学模型谭泽光,姜启源(清华大学,北京100084)捕要:给出奉问题的背景、建模思路、一个具体的确定性数学模型,及相应的计算结果。关■词:公文车调度;运行模型;多目标规划丹赛号:A_Ⅵs(2ooO)90098中国井粪号:TBI14.t空麻标识码:A1问题的背景和要求公交车调度问题的背景是某大城市公交部门提出的一个实际科研课题。该课题要求对一条确定的公交路线,解决三个方面的问题:第一,根据历史积累和必要的补充调查数据,提出沿路各站来站与离站的乘客分布规律;第二,研制一个模拟该线路公交运行过程的数学模型;第三,在前两条的基础上为该线路提出一个配备车辆和司(机)售(票员)人员数目的方案.以及一个在通常情况下车辆的运行时间表。根据这个背景,我们在有关人员的大力支持下,对问题作了大幅度的简化,提出了如下建模问题。首先选择了该市一条比较典型的公交线路,沿线上行方向共14站,下行方向共13站,根据多年来沿线各站乘客来、离站的人数调查数据,给出了该线一个工作日两个运行方向各站上下车的乘客数量按时间的分布。为简单明确起见,同时假设:公交公司配给该线路同一型号的大客车,每辆标准载客100人;客车在该线路上运行的平均速度为20公里/,J、时;并顾及社会效益对运营调度提出的基本要求为:乘客候车时间一般不要超过1O分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%;同时又考虑到提高公交公司运营效益,提出了车辆满载率一般也不要低于50%的指标。问题要求根据上述数据,在尽可能适当考虑公交社会效益和公交公司利益的目标下,为该线路设计一个便于操作的仝天(工作日)的公交车调度方案,即两个起点站的发车时刻表,并指出实现这个方案至少需要配备多少辆车;给出这种方案照顾乘客和公交公司双方的利益程度的数量指标,从而将这个调度问题抽象成一个明确、完整的数学模型,并指出求解模型的方法。2建立模型的思路和框架该调度问题可分成三个子问题:1)建立模拟公交车运营时的运行模型,即在某一确定调度方案下,公交车在该线路上运行过程的数学描述。一种比较切合实际一些的是随机模型,通过随机模拟来模拟运行过程,由维普资讯http://www.cqvip.com工程数学学报第l9卷决策变量及原始数据取得要求的各种目标数值。另一种是建立确定性模型,把运行过程看作一个按一定...