02.笔记小结【公众号：小盆学长】免费分享(3).pdfVIP免费

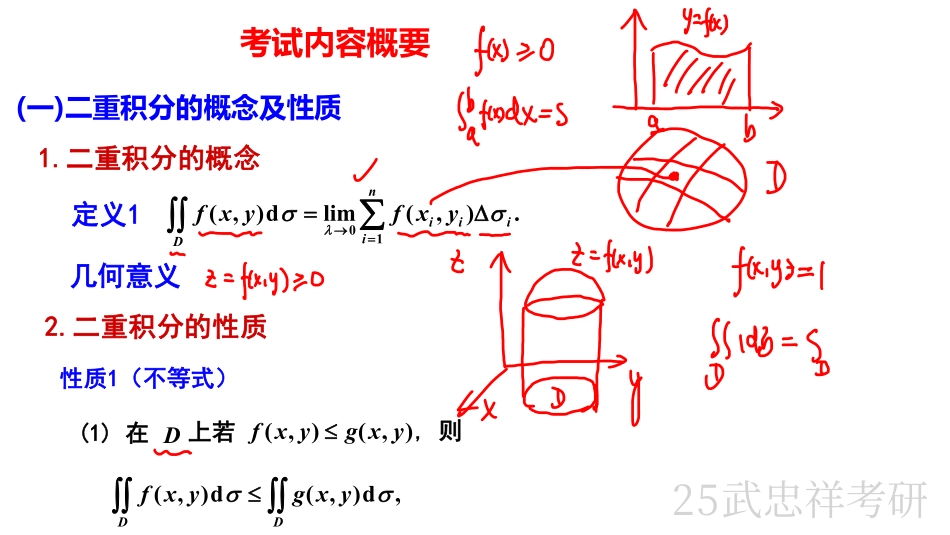
高数基础班（19）19二重积分（概念、性质、计算方法及举例）P150-156主讲武忠祥教授第九章二重积分本章内容要点一.考试内容概要(一）二重积分的概念与性质（二）二重积分计算二.常考题型方法与技巧题型二二重积分计算题型一累次积分交换次序及计算25武忠祥考研考试内容概要(一)二重积分的概念及性质1.二重积分的概念定义1.),(limd),(10niiiiDyxfyxf几何意义2.二重积分的性质性质1（不等式）D),(),(yxgyxf,d),(d),(DDyxgyxf(1)在上若,则25武忠祥考研D,),(Myxfm,d),(MSyxfmSDSD(2)若在上有则其中为区域的面积。.d|),(|d),(3DDyxfyxf）（),(yxfDSDD),,(SfyxfD),(d),(性质2（中值定理）设函数在闭区域上连续，为区域的面积,则在上至少存在一点使得（二)二重积分的计算1．利用直角坐标计算yx)()(21),(d),(xxbaDdyyxfdxyxf1）先后25武忠祥考研xy)()(21),(d),(yydcDdxyxfdyyxf2）先后2．利用极坐标计算)()(21)sin,cos(d),(dfdyxfD1）先后【注】适合用极坐标计算的二重积分的特征（1）适合用极坐标计算的被积函数:);(),(),(22yxfxyfyxf;222Ryx;2222Ryxr;222axyx222;xyby（2）适合用极坐标的积分域:如25武忠祥考研3．利用对称性和奇偶性计算DDyxfyxfyxfyxfyxfdyxfx),(),(;0),(),(;d),(2),(0Dy1)若积分域关于轴对称,则:DDyxfyxfyxfyxfyxfdyxfy),(),(0),(),(d),(2),(0Dx2)若积分域关于轴对称,则:25武忠祥考研4．利用变量对称性计算Dxy`.d),(d),(DDxyfyxf若关于对称,则25武忠祥考研xxdyyxfdx2102),(.___________常考题型的次序1.累次积分交换次序或计算【例1】交换累次积分常考题型与典型例题2.二重积分计算一.累次积分交换次序或计算25武忠祥考研),(yxf212214),(),(xyydxyxfdydyyxfdx2141.),(xdyyxfdx214.),(xxdyyxfdx【例2】(2009年,2)设函数连续,则（A）（B）2141.),(ydxyxfdy212.),(ydxyxfdy（C）（D）（C）25武忠祥考研20cos0d)sin,cos(df1002d),(dyyxyxfy10102d),(dyxyxfy1010d),(dyyxfx1002d),(dxxyyxfx【例3】(1996年,3)累次积分可以写成（B）（C）（D）（A）(D)25武忠祥考研....