2-1导数的定义【公众号：小盆学长】免费分享(1).pdfVIP免费

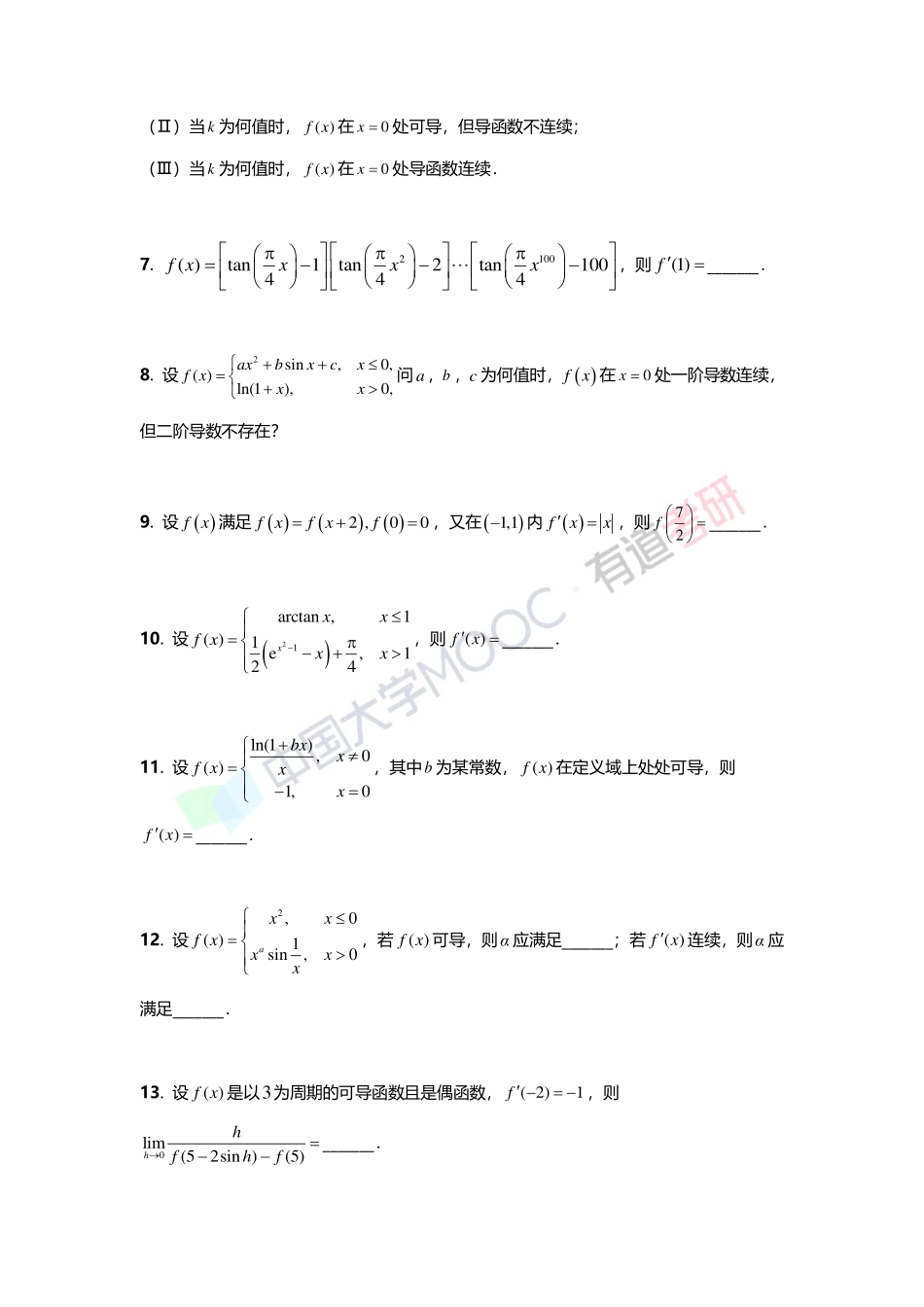
高数强化2-1巩固练习《高数辅导讲义·严选题》P9-12：1，2，3，4，5，6，7，8，18，19，29，33，34综合测试1.设()fx存在，a，b为任意实数，则0()()limxfxaxfxbxx（）．（A）()()xabf.（B）()()xabf.（C）()afx.（D）()bfx.2.设()11xfxx，则fx在0x处（）．（A）连续且可导.（B）右连续但右导数不存在.（C）右连续且右导数存在.（D）右极限存在且右导数存在.3.设()yfx由方程21sind4yxtxt确定，则1lim1nnfn_______．4.设)0(f存在且为正数，101cos()lim1esinxxfxx，则)0(f_______．5.设连续函数()yfx在点(1)0,处满足()yxox，则极限e2301()dlimln1xxfttxx_______．6.设1sin,0,()0,0.kxxfxxx（Ⅰ）当k为何值时，()fx在0x处不可导；（Ⅱ）当k为何值时，()fx在0x处可导，但导函数不连续；（Ⅲ）当k为何值时，()fx在0x处导函数连续．7.2100()tan1tan2tan100444fxxxx，则)1(f_______．8.设2sin,0,()ln(1),0,axbxcxfxxx问a，b，c为何值时，fx在0x处一阶导数连续，但二阶导数不存在？9.设fx满足2,00fxfxf，又在1,1内fxx，则72f_______．10.设21arctan,1()1e,124xxxfxxx，则()fx_______．11.设ln(1),0()1,0bxxfxxx，其中b为某常数，()fx在定义域上处处可导，则()fx_______．12.设2,0()1sin,0axxfxxxx，若()fx可导，则α应满足_______；若()fx连续，则α应满足_______．13.设()fx是以3为周期的可导函数且是偶函数，(2)1f，则0lim(52sin)(5)hhfhf_______．14.设()fx在0x可导且(0)1f，(0)3f，则数列极限111cos1limnnnIfn_______．15.设()fx在xa处二阶导数存在，则0()()()limhfahfafahIh_______．16.（95-3）设2202(1cos),0,()1,0,1cosd,0,xxxxfxxttxx讨论()fx在0x处的连续性和可导性.拓展提升1.设()fx在(1,1)上有定义且为奇函数，当(0,1)x时，cosln(1)()xxxfxx，则函数()fx在0x处（）．（A）左导数不存...