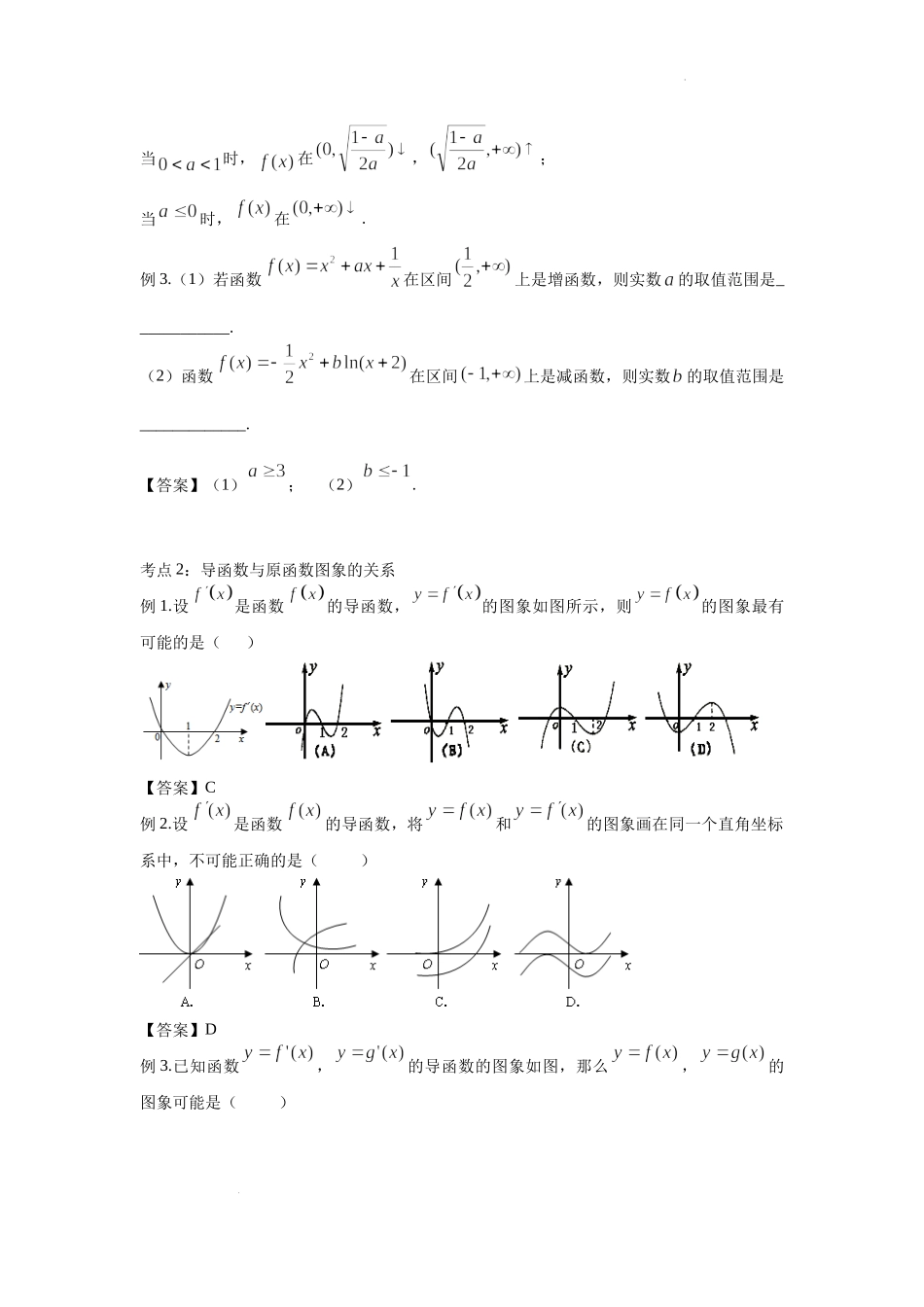
学科网(北京)股份有限公司2.2导数与函数的单调性一.学习目标1.理解导数与函数单调性的关系;2.会利用导数研究函数的单调性问题.二、知识要点1.已知函数在上可导,①若,则函数在区间上递增;②若,则函数在区间上递减.2.已知函数在上可导,①若在上递增,则;②若在上递减,则三、典例分析考点1:用导函数研究原函数的单调性1.求下列函数的单调区间:(1);(2);(3)【答案】(1),,;(2),;(3),.例2.讨论下列函数的单调性:(1);(3).【答案】(1)当时,在,当时,在,,;(2)当时,在;学科网(北京)股份有限公司当时,在,;当时,在.例3.(1)若函数在区间上是增函数,则实数的取值范围是____________.(2)函数在区间上是减函数,则实数的取值范围是_____________.【答案】(1);(2).考点2:导函数与原函数图象的关系例1.设是函数的导函数,的图象如图所示,则的图象最有可能的是()【答案】C例2.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是()【答案】D例3.已知函数,的导函数的图象如图,那么,的图象可能是()学科网(北京)股份有限公司【答案】D考点3.导数与单调性的应用例1.已知奇函数在上是增函数,,若,,,则的大小关系为()A.B.C.D.【答案】C例2.若是定义在上的可导函数,且满足,则必有()A.B.C.D.【答案】D例3.设函数是奇函数的导函数,,当时,,则使得成立的的取值范围是()A.B.C.D.【答案】A四、课外作业1.函数在下面哪个区间上是增函数()A.B.C.D.【答案】B2.若函数f(x)=2x+(a∈R)在[1,+∞)上是增函数,则实数a的取值范围是()A.[0,2]B.[0,4]C.(-∞,2]D.(-∞,4]【答案】C学科网(北京)股份有限公司3.若函数的导函数在区间上是增函数,则函数在区间上的图象可能是()【答案】A4.已知f(x)=,则()A.f(2)>f(e)>f(3)B.f(3)>f(e)>f(2)C.f(3)>f(2)>f(e)D.f(e)>f(3)>f(2)【答案】D.5.函数的导函数的图象如图所示,则函数的图象可能是()【答案】B6.已知是可导函数,且对,,,则有()A.,B.,C.,D.,【答案】A7.已知定义在区间(-π,π)上的函数,则的单调递增区间是________.【答案】和8.已知在上是减函数,则实数的取值范围是__________.【答案】学科网(北京)股份有限公司9.已知函数,其中是自然对数的底数,若,则实数的取值范围是___________.【答案】10.设函数,曲线在点处的切线方程.(1)求的值;(2)求的单调区间.【答案】...