微电子器件 （习题解答）.pptVIP免费

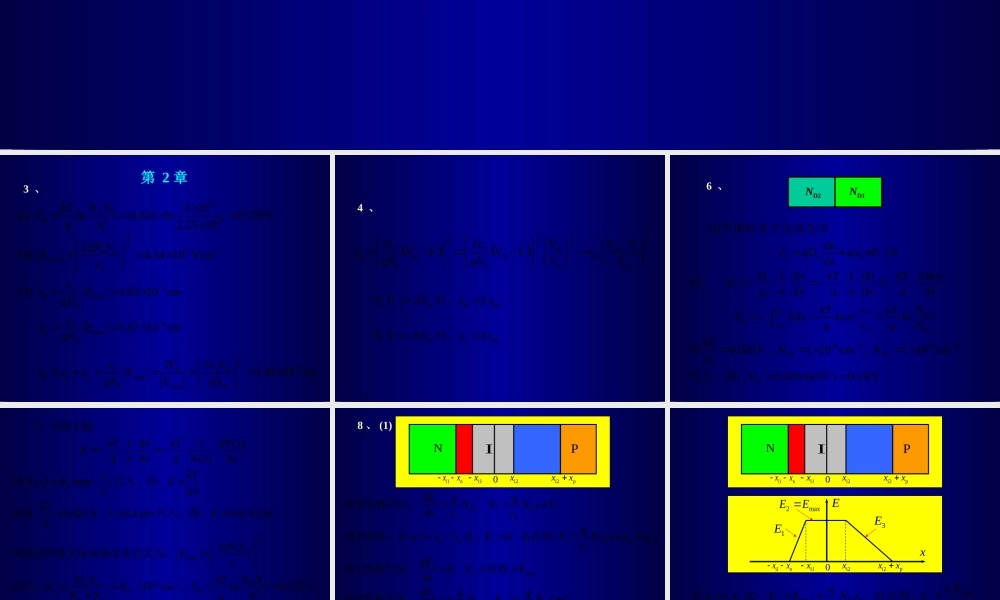
部分习题解答部分习题解答3、32ADbi220i510(1)ln0.026ln0.739V2.2510NNkTVqn5SpmaxA6SnmaxD125SbiSbidpnmax0max0(2)2.8310cm5.6710cm223.4010cmxEqNxEqNVVxxxEqNEqN124-10bimaxS2(3)4.3410VcmqNVE第2章4、11112222SSbibidbibid000bibi22VVVxVVVVxqNqNVVbidd032VVxx当时，bidd083VVxx当时，d1D1d2D2nnnnnD1biD2203163D1D24bid0d1d1ddlnddddln|ln0.026V,110cm,110cm0.026ln(10)0.24VxNxNnJqDqnExDnkTnkTnEnxqnxqxNkTkTVExnqqNkTNNqV由平衡时多子电流为零得：将代入，得：6、ND2ND10120bimaxs153DADA0Dbi2DAi761d1d()d()d()exp()0.026V,0.4μm650Vcm2||10cm,ln0.757V,1.610kTnkTNxEqnxqNxxxkTNxNEqkTEqqNVENNNNkTNNVNNqnq、由第题：将代入，得：再将代入，得：突变结的最大电场强度表达式为：式中：1912S4maxmaxC,1.04510Fcm,||||1.5210VcmEE代入中，得：1D1D1i1n11Di1ns22max3A3A3ssi2p33Ai2psdN,d0()dI0,ddP,d0()ssEqqNENxCxqxxxEENxxxEEExEqqNENxCxqxxxEENxxx在型耗尽区，边界条件：在处，，由此得：在型耗尽区，常数在型耗尽区，边界条件：在处，，由此得：8、(1)0i1xi1nxxi2xi2pxxNIPsmaxi11maxDnnsDsmaxi23maxAppsA,,EqxxEENxxqNEqxxEENxxqN在处，由此得：在处，由此得：i2xi1x0E1E2maxEE3Ex0i1xi1nxxi2xi2pxxNIPi2pxxi1nxxi1i21Dn3ApsmaxDnApssIPN0,0,(),()0sqqxxENxxENxxqqxENxNx对于无型区的结,在处，电场达到最大，(2)maxbinpmaxEVxxE表面上，两种结构的的表达式相同，但由于两种结构的掺杂相同，因而相同（即电场曲线与横轴所围面积相同），所以两种结构的、与并不相同。0E1EmaxE3ExppApAnnDnD2pidppD2nidnnAdpnpApAndnpnDpnD1exp1exp11qNNqNNqDnqVJLNkTqDnqVJLNkTJLDNNLJLDNLN已知：由于因此20、24、PN结的正向扩散电流为0expqVIIkT式中的...