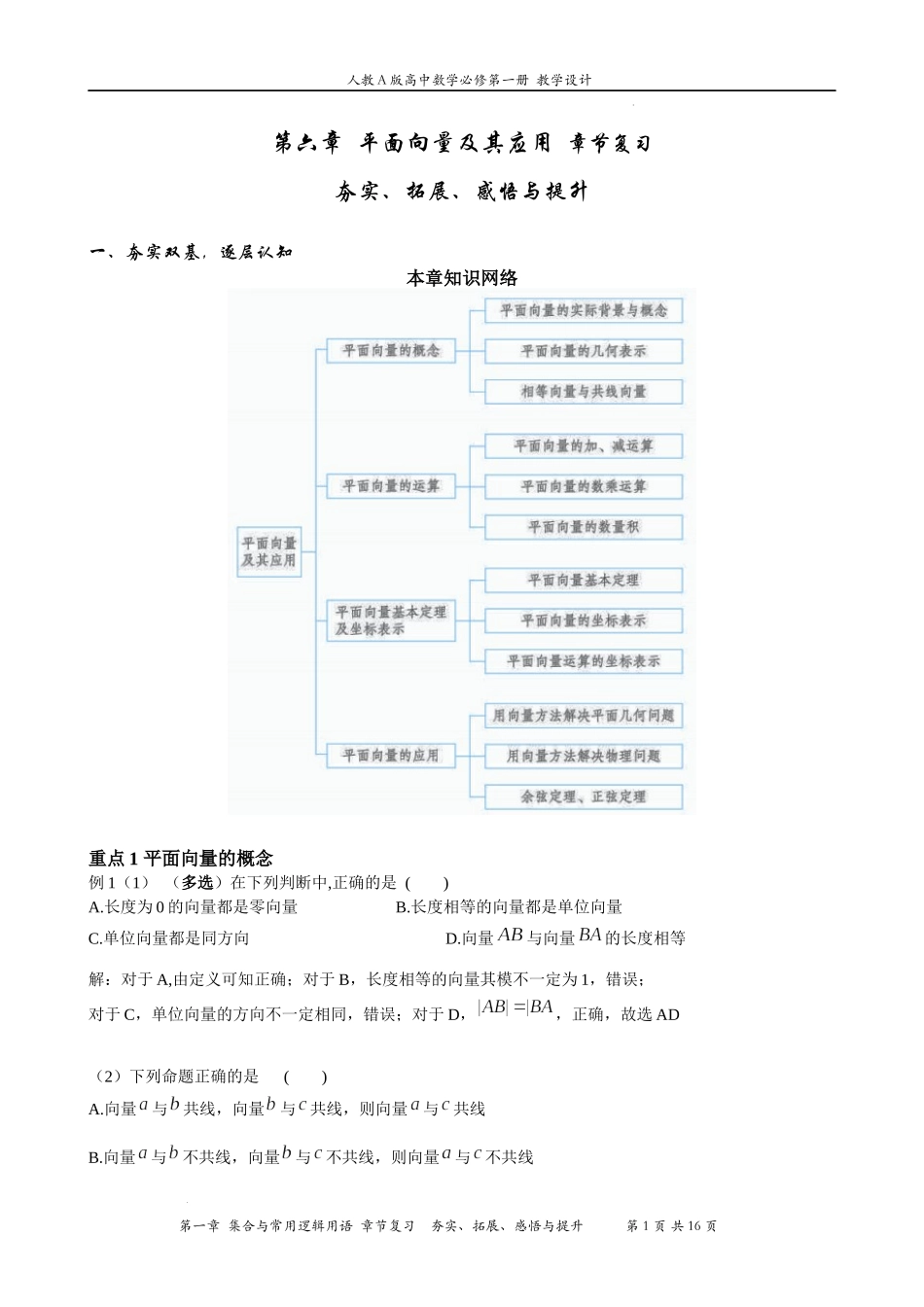
人教A版高中数学必修第一册教学设计第一章集合与常用逻辑用语章节复习夯实、拓展、感悟与提升第1页共16页学科网(北京)股份有限公司第六章平面向量及其应用章节复习夯实、拓展、感悟与提升一、夯实双基,逐层认知本章知识网络重点1平面向量的概念例1(1)(多选)在下列判断中,正确的是()A.长度为0的向量都是零向量B.长度相等的向量都是单位向量C.单位向量都是同方向D.向量与向量的长度相等解:对于A,由定义可知正确;对于B,长度相等的向量其模不一定为1,错误;对于C,单位向量的方向不一定相同,错误;对于D,,正确,故选AD(2)下列命题正确的是()A.向量与共线,向量与共线,则向量与共线B.向量与不共线,向量与不共线,则向量与不共线人教A版高中数学必修第一册教学设计第一章集合与常用逻辑用语章节复习夯实、拓展、感悟与提升第2页共16页学科网(北京)股份有限公司C.向量与是共线向量,则四点一定共线D.向量与不共线,则与都是非零向量解:当时,A错误;如图,,,都与不共线,但与共线,B错误;在中,与共线,但四点不共线,C错;若与有一个为零向量,则与一定共线,所以与不共线时,一定有与都是非零向量,故选D.重点2平面向量的运算例2(1)在中,点在直线的延长线上,且,则()A.0B.C.D.3解:因为,所以,又,所以,所以,故选C(2)已知向量,且,则一定共线的三点是()A.B.C.D.解:因为,所以共线,故选A(3)在中,,则()A.B.C.8D.16解:设,则,又所以,故选D(4)若向量满足,则_____.人教A版高中数学必修第一册教学设计第一章集合与常用逻辑用语章节复习夯实、拓展、感悟与提升第3页共16页学科网(北京)股份有限公司解:由已知,所以,即,即所以,解得答案:.(5)已知向量,满足,,,则向量与向量的夹角的余弦值等于()A.B.C.D.解:设向量与向量的夹角为,由已知,又,所以因此,.故选D.(6)点是所在平面上的一点,且满足,则点是的()A.重心B.垂心C.内心D.外心解:因为,所以,即,所以,同理,所以点是的垂心,故选B.重点3平面向量基本定理及坐标表示例3(1)在平行四边形中,分别是和的中点.若,其中,则__________.解:方法一:选择作为平面向量的一个基底,则,又人教A版高中数学必修第一册教学设计第一章集合与常用逻辑用语章节复习夯实、拓展、感悟与提升第4页共16页学科网(北京)股份有限公司所以,解得所以方法二:如图,连结交于,因为和分别是边和的中点,所以为的中点,也是的四等分点,且又,于是,所以因此答案:(2)在...