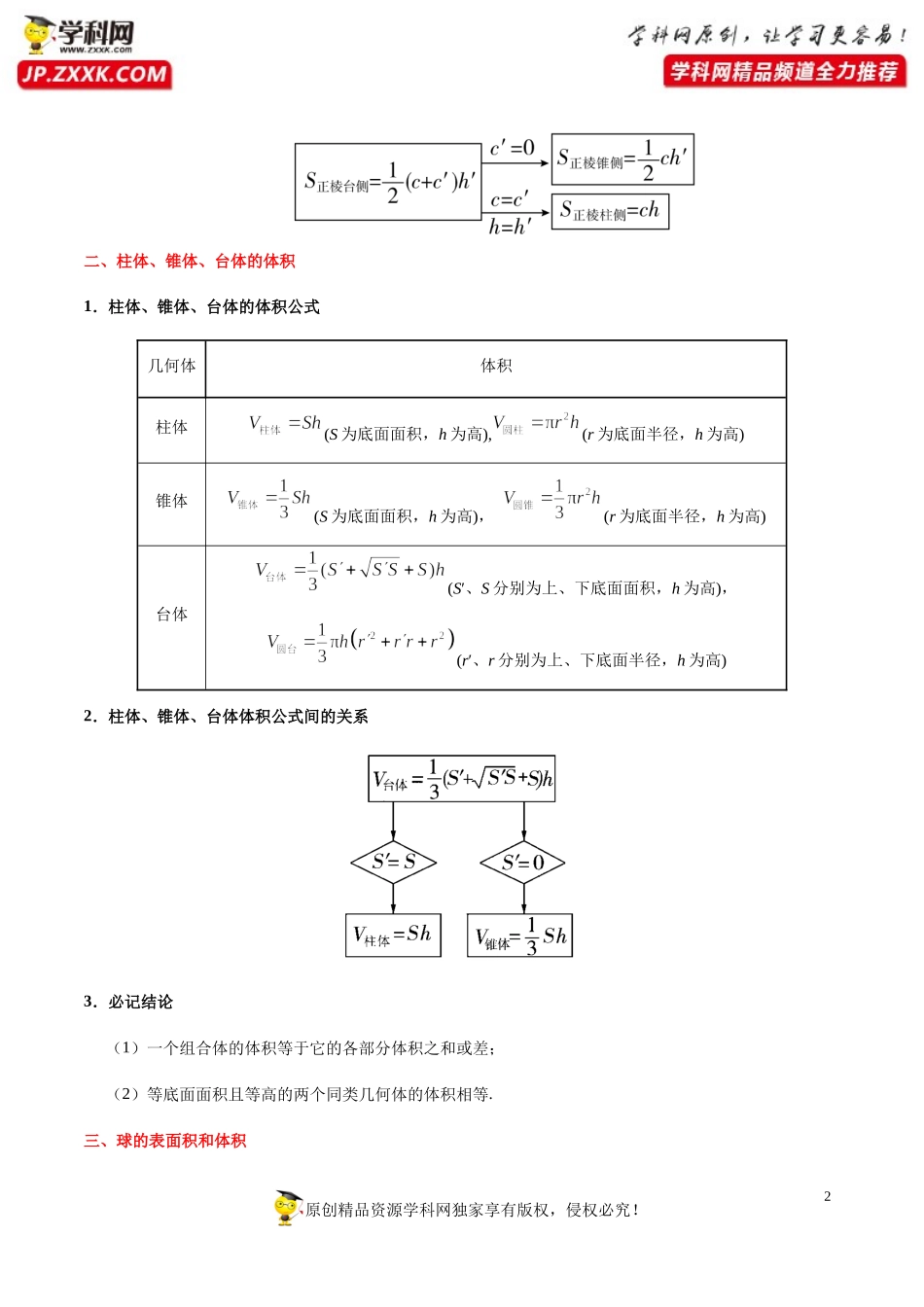
1原创精品资源学科网独家享有版权,侵权必究!考点28空间几何体的表面积与体积空间几何体的表面积与体积的求解是高考的重点,会单纯出现在选择题或填空题中,我们要重点了解球、棱柱、棱锥、台的表面积和体积的计算公式.一、柱体、锥体、台体的表面积1.旋转体的表面积圆柱(底面半径为r,母线长为l)圆锥(底面半径为r,母线长为l)圆台(上、下底面半径分别为r′,r,母线长为l)侧面展开图底面面积侧面面积表面积2.多面体的表面积多面体的表面积就是各个面的面积之和,也就是展开图的面积.棱锥、棱台、棱柱的侧面积公式间的联系:2原创精品资源学科网独家享有版权,侵权必究!二、柱体、锥体、台体的体积1.柱体、锥体、台体的体积公式几何体体积柱体(S为底面面积,h为高),(r为底面半径,h为高)锥体(S为底面面积,h为高),(r为底面半径,h为高)台体(S′、S分别为上、下底面面积,h为高),(r′、r分别为上、下底面半径,h为高)2.柱体、锥体、台体体积公式间的关系3.必记结论(1)一个组合体的体积等于它的各部分体积之和或差;(2)等底面面积且等高的两个同类几何体的体积相等.三、球的表面积和体积3原创精品资源学科网独家享有版权,侵权必究!1.球的表面积和体积公式设球的半径为R,它的体积与表面积都由半径R唯一确定,是以R为自变量的函数,其表面积公式为,即球的表面积等于它的大圆面积的4倍;其体积公式为.2.球的切、接问题(常见结论)(1)若正方体的棱长为,则正方体的内切球半径是;正方体的外接球半径是;与正方体所有棱相切的球的半径是.(2)若长方体的长、宽、高分别为,,,则长方体的外接球半径是.(3)若正四面体的棱长为,则正四面体的内切球半径是;正四面体的外接球半径是;与正四面体所有棱相切的球的半径是.(4)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径.(5)球与圆台的底面与侧面均相切,则球的直径等于圆台的高.考向一柱体、锥体、台体的表面积1.已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.2.多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理,以确保不重复、不遗漏.4原创精品资源学科网独家享有版权,侵权必究!3.求多面体的侧面积时,应对每一个侧面分别求解后再相加;求旋转体的侧面积时,一般要将旋转体展开为平面图形后再求面积.典例1某几何体的三视...