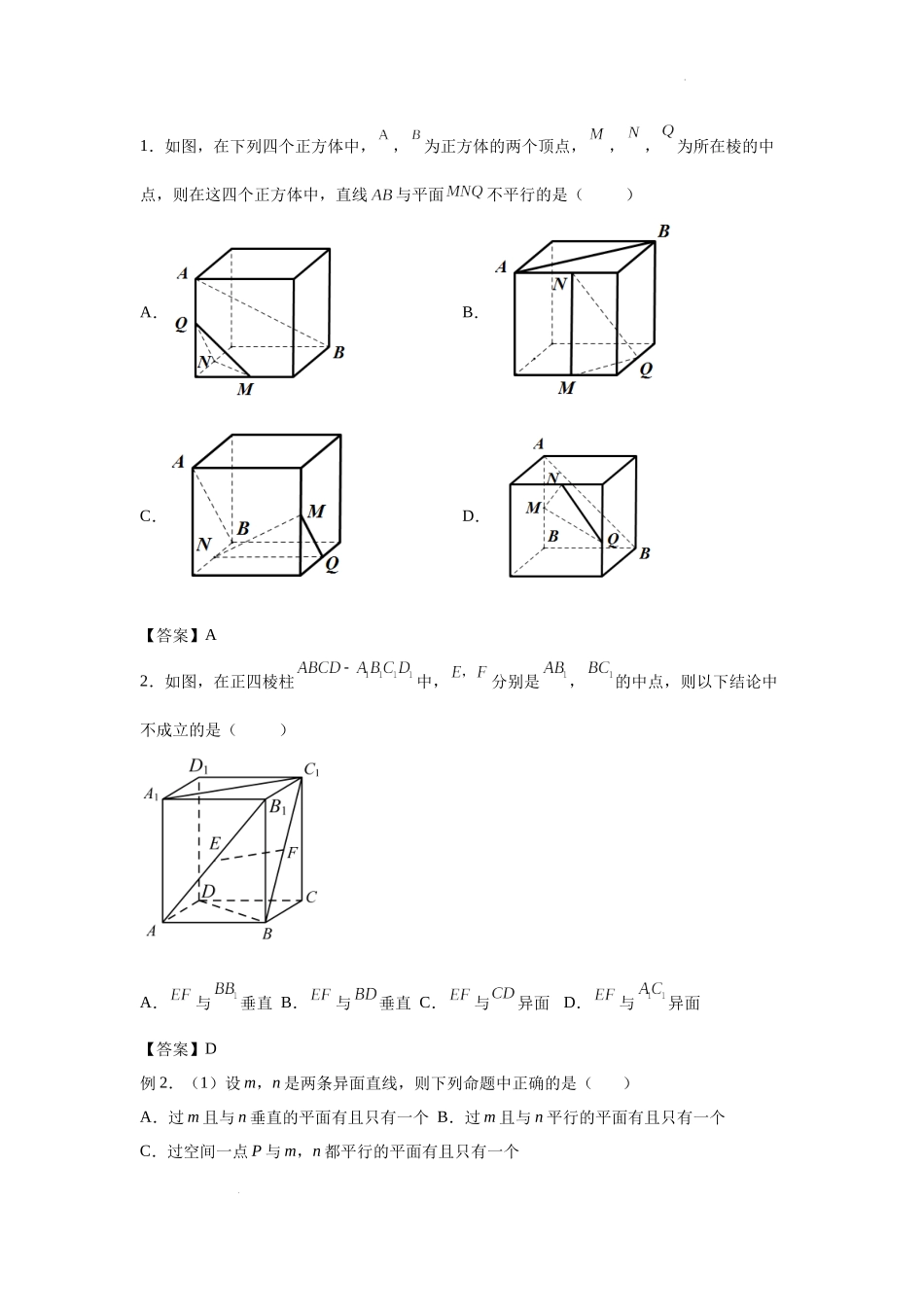
学科网(北京)股份有限公司第14讲空间点、线、面的位置关系一、学习目标1.掌握空间中的点、线、面的位置关系的判定;2.掌握平面与垂直关系的判定与证明.二、典例分析例1.(1)如图,在正方体中,P是线段上的动点,则()A.平面B.平面C.平面D.平面(2)2.如图已知正方体,M,N分别是,的中点,则()A.直线与直线垂直,直线平面B.直线与直线平行,直线平面C.直线与直线相交,直线平面D.直线与直线异面,直线平面【答案】(1)B;(2)A变式:学科网(北京)股份有限公司1.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面不平行的是()A.B.C.D.【答案】A2.如图,在正四棱柱中,分别是,的中点,则以下结论中不成立的是()A.与垂直B.与垂直C.与异面D.与异面【答案】D例2.(1)设m,n是两条异面直线,则下列命题中正确的是()A.过m且与n垂直的平面有且只有一个B.过m且与n平行的平面有且只有一个C.过空间一点P与m,n都平行的平面有且只有一个学科网(北京)股份有限公司D.过空间一点P与m,n都垂直的平面有且只有一个(2)如图,平面α与平面β相交于BC,ABα⊂,CDβ⊂,点A∉BC,点D∉BC,则下列叙述错误的是()A.直线AD与BC异面B.过AD只有唯一平面与BC平行C.过点D只能作唯一平面与BC垂直D.过AD一定能作一平面与BC垂直【答案】(1)B;(2)D.变式:1.已知圆锥SO,AB是圆O的直径,P是圆O上一点(不与A,B重合),Q在平面SAB上,则()A.直线可能与平面垂直B.直线可能与平面垂直C.直线可能与平面平行D.直线可能与平面平行【答案】C2.在正方体ABCDA1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线()A.不存在B.有且只有两条C.有且只有三条D.有无数条【答案】D例3.如图,在四棱锥中,平面,.(Ⅰ)求证:;(Ⅱ)求证:;(Ⅲ)设点E为AB的中点,在棱PB上是否存在点F,使得平面?说明理由.学科网(北京)股份有限公司【答案】(Ⅰ)因为平面,所以.又因为,所以平面.(Ⅱ)因为,,所以.因为平面,所以.所以平面.所以平面平面.(Ⅲ)棱PB上存在点F,使得平面.证明如下:取PB中点F,连结EF,,.又因为E为的中点,所以.又因为平面,所以平面.变式:1.如图,在四棱锥中,平面平面,,,,,,.(1)求证:平面;(2)在棱上是否存在点,使得平面?若存在,求的值;若不存在,说明理由.学科网(北京)股份...