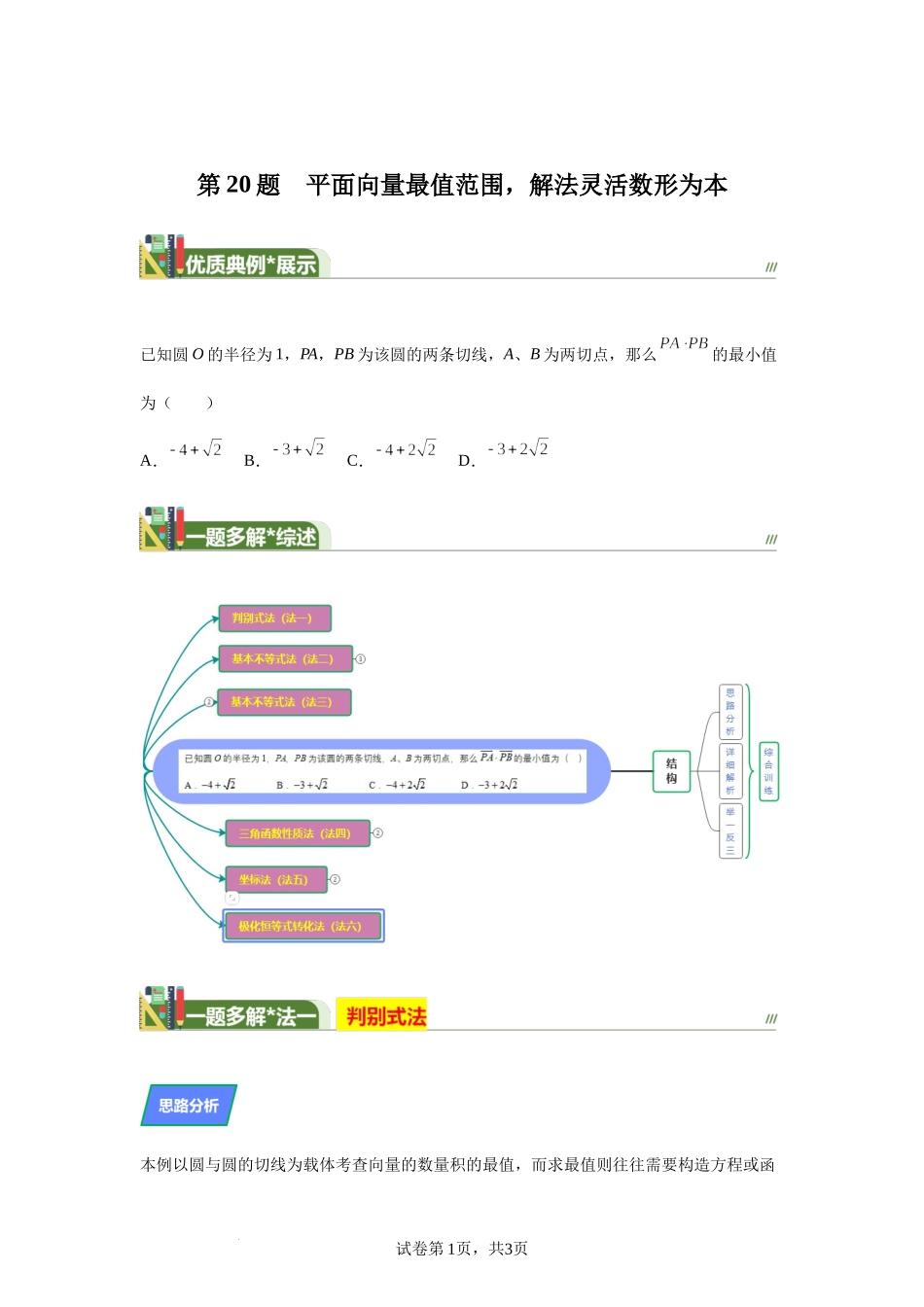
试卷第1页,共3页学科网(北京)股份有限公司第20题平面向量最值范围,解法灵活数形为本已知圆O的半径为1,PA,PB为该圆的两条切线,A、B为两切点,那么的最小值为()A.B.C.D.本例以圆与圆的切线为载体考查向量的数量积的最值,而求最值则往往需要构造方程或函试卷第2页,共3页数,如何引进变量就显得非常重要.思路一是以切线长为变量x,将可表示为x的函数,再转化为方程用判别式法求解,如图20-1所示,设(),,则.,,令,则.即, 是实数,∴,即,解得或故,此时,故选D.试卷第3页,共3页学科网(北京)股份有限公司1.设,为单位向量,非零向量,.若,的夹角为,则的最大值等于.本例以圆与圆的切线为载体考查向量的数量积的最值,而求最值则往往需要构造方程或函数,如何引进变量就显得非常重要.思路二是以OP长为变量r,将表示为关于的函数,借助基本不等式求解.如图20-2所示,设,,则,.∴有,当且仅试卷第4页,共3页当时等号成立.∴,故选D.(2023·天津·统考高考真题)2.在中,,,记,用表示;若,则的最大值为.本例以圆与圆的切线为载体考查向量的数量积的最值,而求最值则往往需要构造方程或函数,如何引进变量就显得非常重要.思路三是以O到AB中点M的距离为变量,将表示为关于的函数(利用向量运算三角形法则和直角三角形射影定理求得),借助基本不等式求解.如图20-3所示,设AB的中点为M且,在中,由直角三角形射影定理有,.∴,.试卷第5页,共3页学科网(北京)股份有限公司∴.当且仅当时等号成立,∴,故选D.(2024·全国·模拟预测)3.已知非零且不垂直的平面向量,满足,若在方向上的投影与在方向上的投影之和等于,则,夹角的余弦值的最小值为.本例以圆与圆的切线为载体考查向量的数量积的最值,而求最值则往往需要构造方程或函数,如何引进变量就显得非常重要.思路四是引进为变量,将表示为三角函数,原问题进入了三角函数这一知识板块,应用三角恒等变换、三角函数的性质以及换元法求解.试卷第6页,共3页设,.则令,,,故选D.4.如图,已知等腰直角三角形中,,,两顶点分别在正半轴(含原点)上运动,分别是的中点,则的取值范围是.本例以圆与圆的切线为载体考查向量的数量积的最值,而求最值则往往需要构造方程或函数,如何引进变量就显得非常重要.思路五是建立适当地平面直角坐标系,利用向量数量试卷第7页,共3页学科网(北京)股份有限公司积的坐标运算,建立关于坐标的函数式,再求最小...