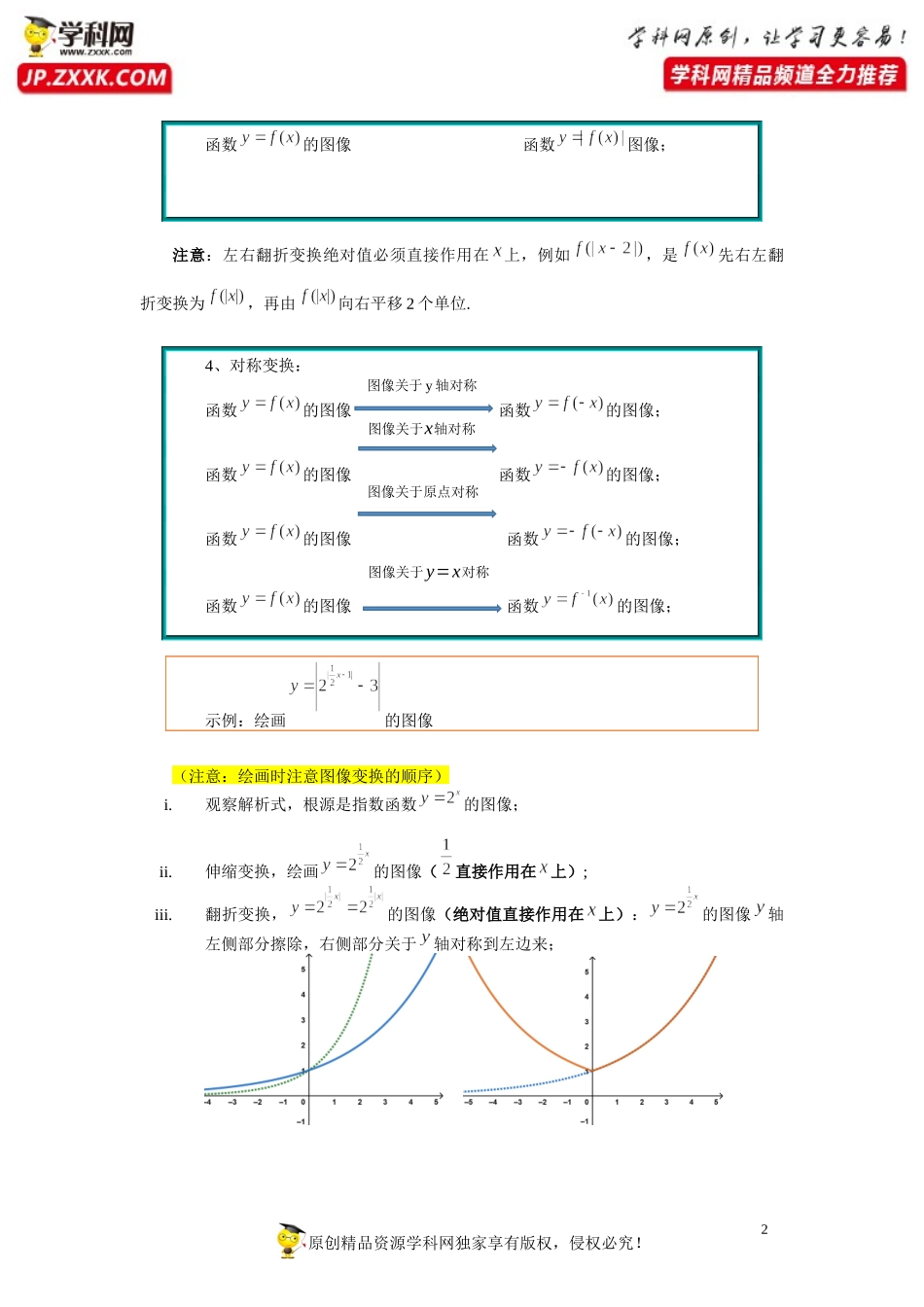
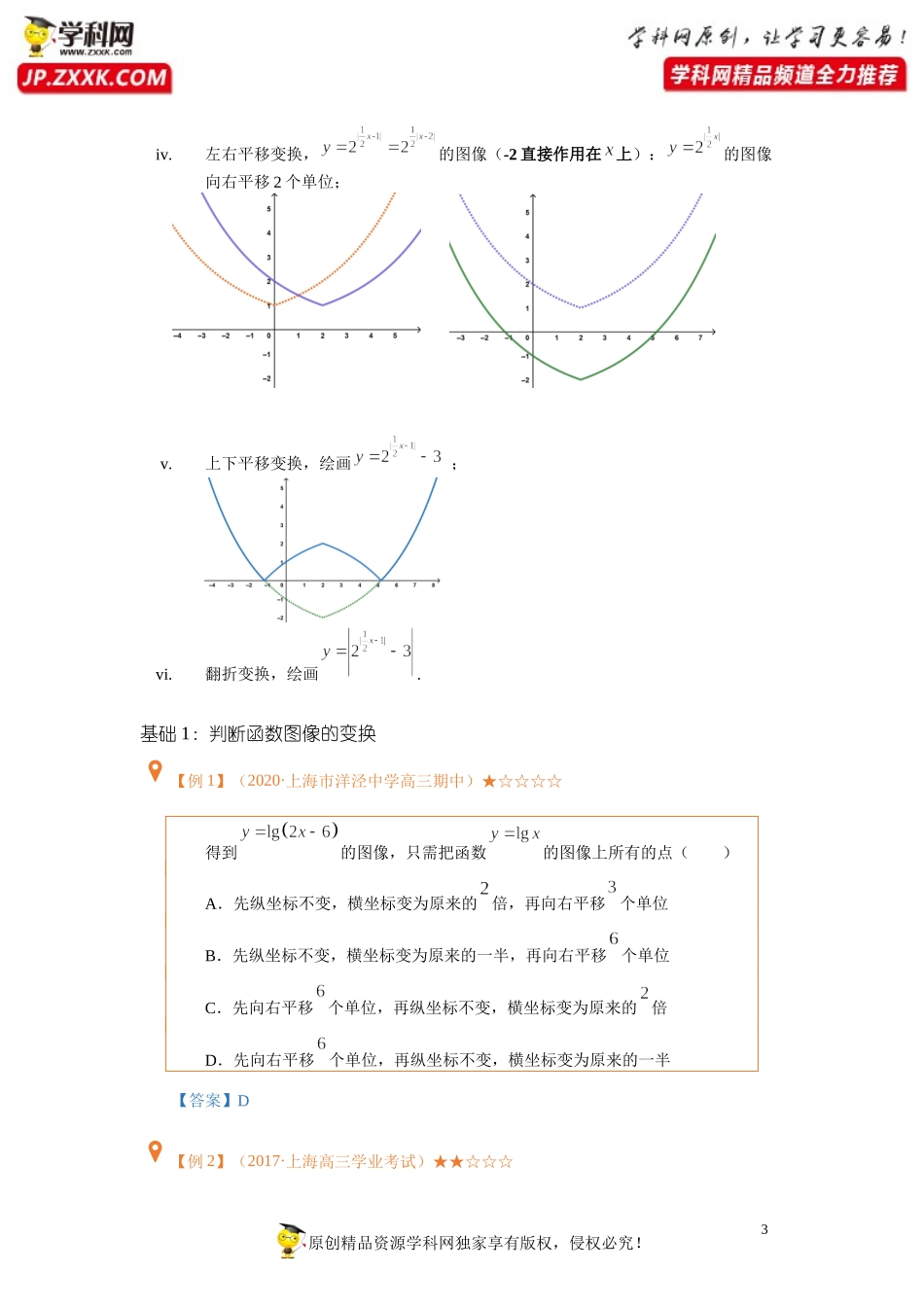
1原创精品资源学科网独家享有版权,侵权必究!知识梳理与题型整理主要考察一:函数图像的变换1、平移变换:函数的图像函数的图像;函数的图像函数的图像;注意:左右平移必须直接作用在上,例如,是向右平移1个单位.2、伸缩变换:函数的图像函数的图像;函数的图像函数的图像;3、翻折变换:函数的图像函数图像;第15讲函数的图像专题(一)左加右减y坐标不变,x坐标伸缩为原来的1/k(k>0)x坐标不变,y坐标伸缩为原来的k倍(k>0)y轴左侧清除,右侧对称到左侧x轴下方翻折到上方,上方保留上加下减2原创精品资源学科网独家享有版权,侵权必究!函数的图像函数图像;注意:左右翻折变换绝对值必须直接作用在上,例如,是先右左翻折变换为,再由向右平移2个单位.4、对称变换:函数的图像函数的图像;函数的图像函数的图像;函数的图像函数的图像;函数的图像函数的图像;示例:绘画的图像(注意:绘画时注意图像变换的顺序)i.观察解析式,根源是指数函数的图像;ii.伸缩变换,绘画的图像(直接作用在上);iii.翻折变换,的图像(绝对值直接作用在上):的图像轴左侧部分擦除,右侧部分关于轴对称到左边来;图像关于y轴对称图像关于y=x对称图像关于x轴对称图像关于原点对称3原创精品资源学科网独家享有版权,侵权必究!iv.左右平移变换,的图像(-2直接作用在上):的图像向右平移2个单位;v.上下平移变换,绘画;vi.翻折变换,绘画.基础1:判断函数图像的变换【例1】(2020·上海市洋泾中学高三期中)★☆☆☆☆得到的图像,只需把函数的图像上所有的点()A.先纵坐标不变,横坐标变为原来的倍,再向右平移个单位B.先纵坐标不变,横坐标变为原来的一半,再向右平移个单位C.先向右平移个单位,再纵坐标不变,横坐标变为原来的倍D.先向右平移个单位,再纵坐标不变,横坐标变为原来的一半【答案】D【例2】(2017·上海高三学业考试)★★☆☆☆4原创精品资源学科网独家享有版权,侵权必究!下列函数中,图像为下图的是()A.B.C.D.【答案】B【详解】由图像可知:定义在上的偶函数,对于AC,为非奇非偶函数,可排除AC;对于D,当时,,与图像不符,可排除D;对于B,,可知图像与函数相符,B正确.故选:B.【练习】(2019秋•浦东新区校级期中)★★☆☆☆将函数的图像上的所有点的纵坐标不变,横坐标伸长到原来的2倍,然后再将所得图像经过怎样的变换才能得到的图像A.向左平移4个单位B.向右平移4个单位5原创精品资源学科网独家享有版权,侵权必究!C...