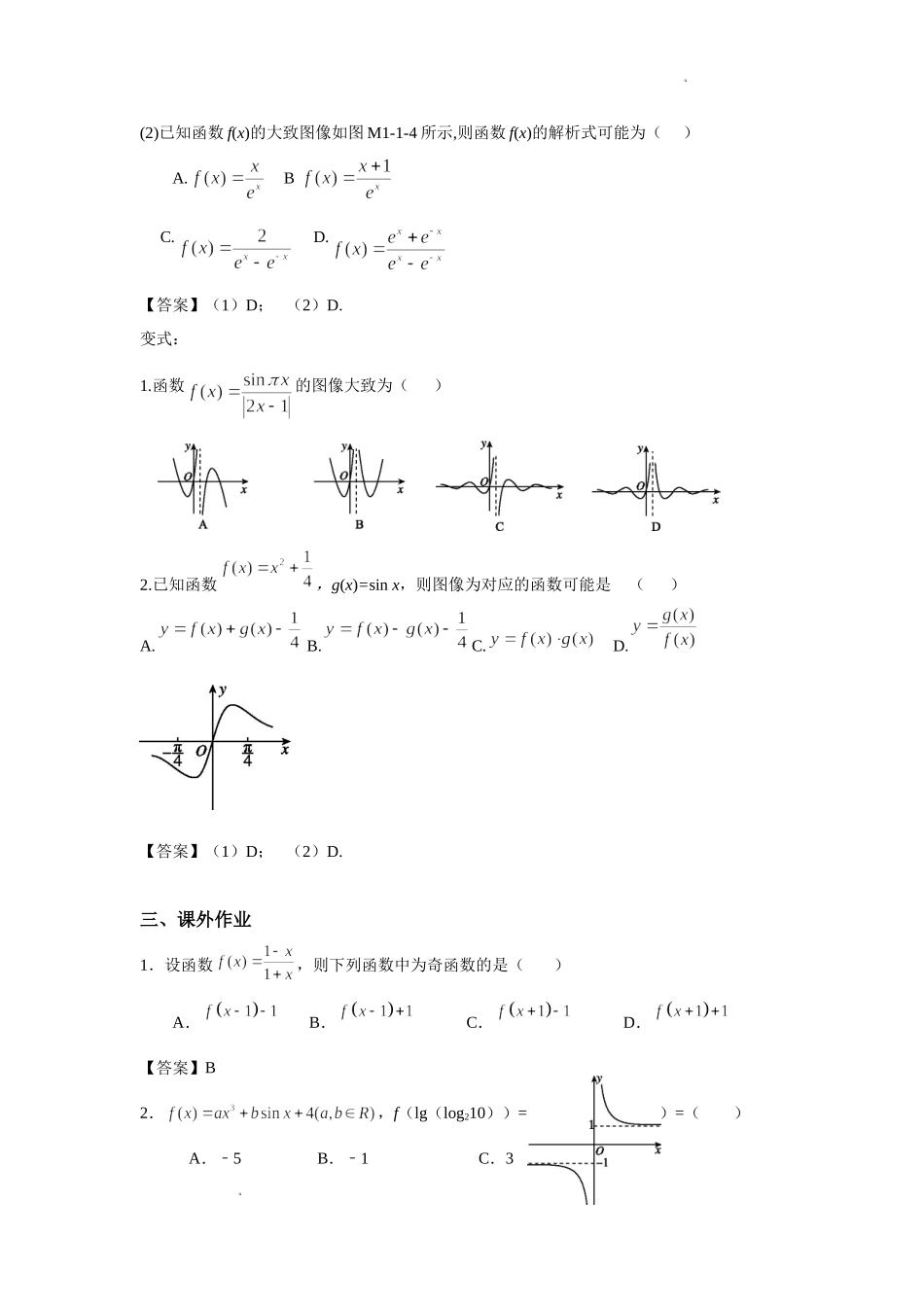
第1讲函数的性质与图象一、学习目标1.理解函数单调性、奇偶性、周期性的概念,并能用以上性质解决一些相关问题;2.会处理与分段函数相关的求值、方程与不等式问题;3.了解抽象函数中的性质运用.二、典例分析例1.(1)已知函数f,则f[f(2)]=_______;关于x的不等式f(x-1)+f(x)≤0的解集为____________.(2)已知函数,f(x1)=f(x2),则|x1-x2|的取值范围是____________.【答案】(1);(2).变式:1.设函数10()20xxxfxx,,,则满足1()12fxfx的x的取值范围是_________.【答案】1,42.若函数则______,不等式的解集为_____________.【答案】,.例2.(1)设函数,则()A.是奇函数,且在(0,+∞)单调递增B.是奇函数,且在(0,+∞)单调递减C.是偶函数,且在(0,+∞)单调递增D.是偶函数,且在(0,+∞)单调递减【答案】A(2)已知函数,则使得成立的的取值范围是()A.B.C.D.【答案】A学科网(北京)股份有限公司变式:1.设函数,则f(x)()A.是偶函数,且在单调递增B.是奇函数,且在单调递减C.是偶函数,且在单调递增D.是奇函数,且在单调递减2.已知函数,若,则实数a的取值范围是___________.【答案】(1)D;(2).例3.(1)设函数的定义域为R,为奇函数,为偶函数,当时,.若,则()A.B.C.D.(2)已知函数f(x)的定义域为R,且f(x+2)是偶函数,f(2x+1)是奇函数,则下列选项中值一定为0的是()A.B.C.D.【答案】(1)D;(2)B.变式:1.函数的定义域,若和都是偶函数,则()A.是偶函数B.是奇函数C.D.【答案】C例4.(1)函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)的大致图像是()学科网(北京)股份有限公司(2)已知函数f(x)的大致图像如图M1-1-4所示,则函数f(x)的解析式可能为()A.BC.D.【答案】(1)D;(2)D.变式:1.函数的图像大致为()2.已知函数,g(x)=sinx,则图像为对应的函数可能是()A.B.C.D.【答案】(1)D;(2)D.三、课外作业1.设函数,则下列函数中为奇函数的是()A.B.C.D.【答案】B2.,f(lg(log210))=5,则f(lg(lg2))=()A.﹣5B.﹣1C.3D.4学科网(北京)股份有限公司【答案】C3.已知函数,若,则()A.B.C.D.【答案】D4.函数在的图像大致为()A.B.C.D.【答案】B5.已知函数的部分图象如右图所示,则可能的解析式是()A.B.C.D.【答案】B6.已知函数是定义在R上的偶函数,且在区间单调递增.若实数满足,则的取值范围是()A.B.C.D.【答案】C7...