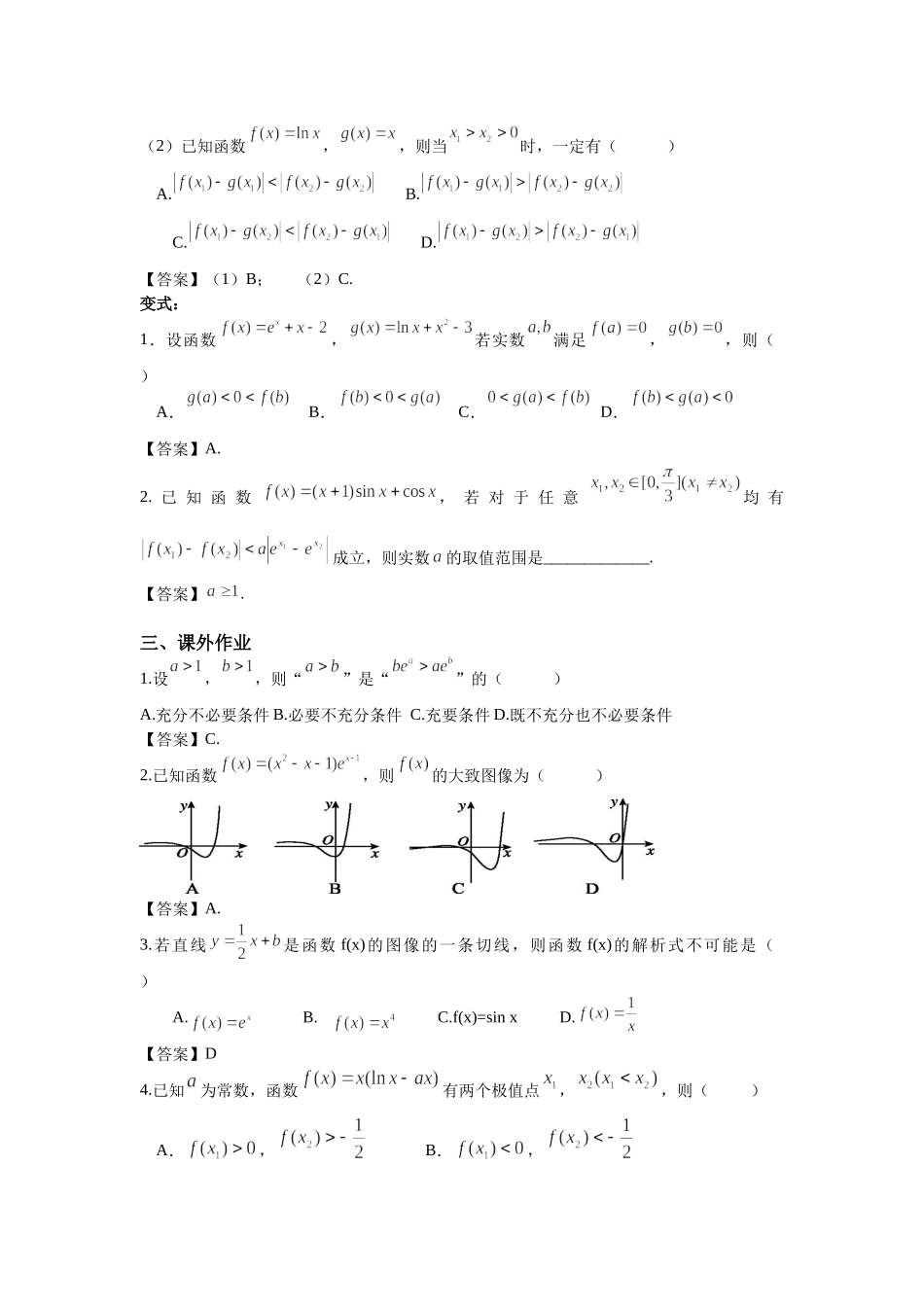
第5讲导数的应用一、学习目标1.理解导数的几何意义,会用导数研究曲线的切线问题;2.理解导数与函数单调性的关系,并会用导数研究函数的极值、最值问题.3.会用导数处理函数的不等式与零点问题.二、典例分析例1.(1)已知直线与曲线相切,则的值为()A.1B.2C.D.(2)已知函数,若过点存在3条直线与曲线相切,则实数的取值范围是____________.(3)直线与曲线相切,也与曲线相切(其中为自然对数的底数),则__________.【答案】(1)B;(2);(3).变式:1.若过点可以作曲线的两条切线,则()A.B.C.D.【答案】D2.若函数与的图像存在公切线,则实数的最小值为________.【答案】.例2.(1)若函数在区间上单调递减,则实数的取值范围是()A.B.C.[1,+∞)D.(2)已知函数有两个极值点,则实数的取值范围是____________.【答案】(1)D;(2).变式:1.设,若函数,,有大于零的极值点,则()A.B.C.D.【答案】A.2.点是曲线上的点,是直线上的点,则的最小值为_______.【答案】.例3.(1)已知函数,若函数有4个零点,则实数的取值范围是_____________.(2)关于的不等式恰有一个整数解,则实数的取值范围是__________.【答案】(1);(2).变式:1.已知函数,,若函数有三个零点,则实数的取值范围是______________.【答案】.2.设函数,其中,若存在唯一的整数,使得,则的取值范围是______________.【答案】.例4.(1)已知正实数,满足,则()A.B.C.D.(2)已知函数,,则当时,一定有()A.B.C.D.【答案】(1)B;(2)C.变式:1.设函数,若实数满足,,则()A.B.C.D.【答案】A.2.已知函数,若对于任意均有成立,则实数的取值范围是_____________.【答案】.三、课外作业1.设,,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C.2.已知函数,则的大致图像为()【答案】A.3.若直线是函数f(x)的图像的一条切线,则函数f(x)的解析式不可能是()A.B.C.f(x)=sinxD.【答案】D4.已知为常数,函数有两个极值点,,则()A.,B.,C.,D.,【答案】D.5.已知函数与图象上存在关于轴对称的点,则的取值范围是()A.B.C.D.【答案】B.6.若是函数的极值点,则的极小值为________.【答案】.7.若函数是自然对数的底数在的定义域上单调递增,则称函数具有性质,下列函数中所有具有性质的函数的序号为__________.①;②;③;④.【答案】①④.8.已知函数,若存在唯一的零点,且,则的取值范...