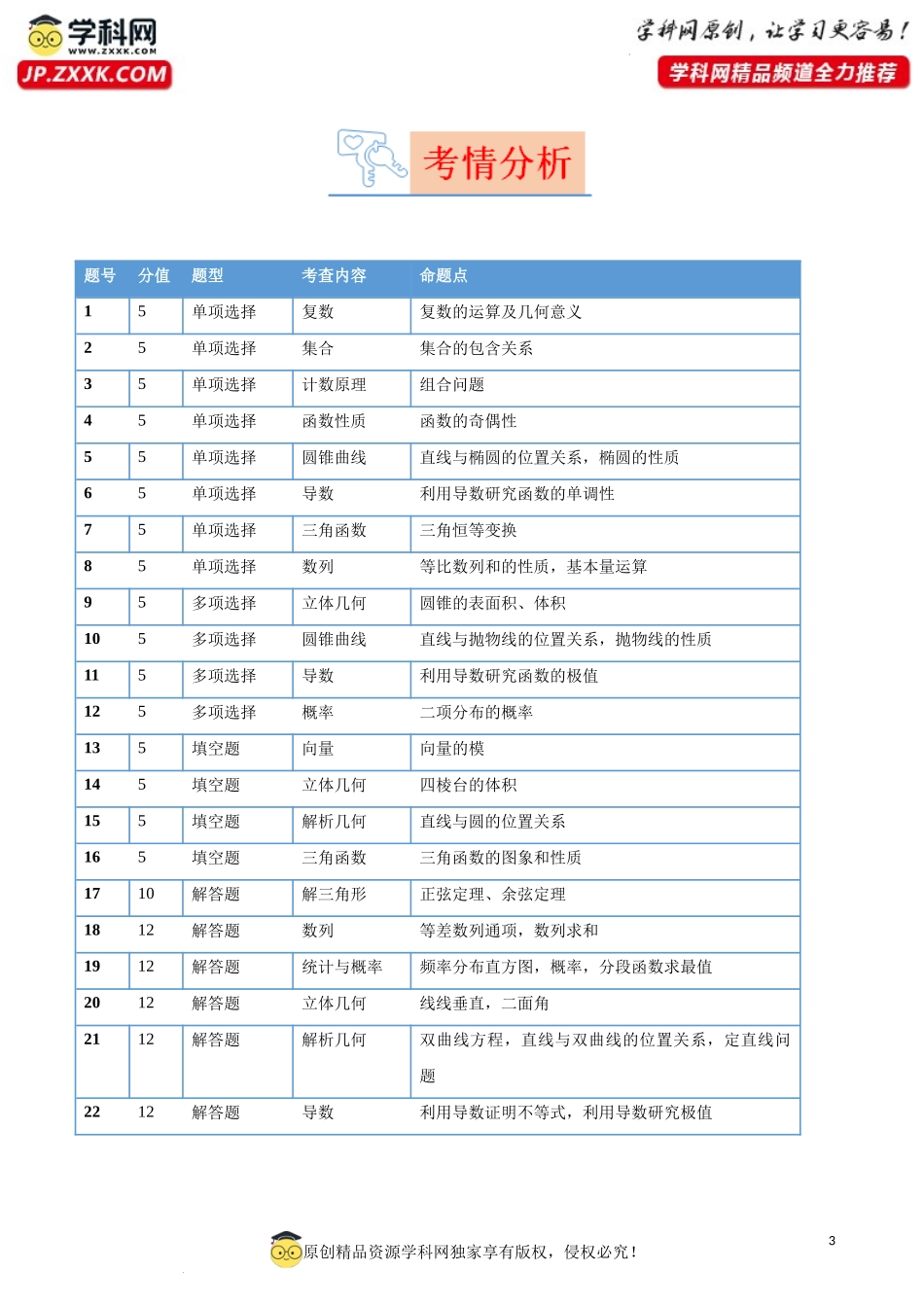
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司2023年高考真题完全解读(新高考Ⅱ卷)适用省份:辽宁、重庆、海南、云南、吉林、黑龙江、安徽、山西一、试卷总体情况分析新高考Ⅱ卷函数与导数四个小题,一个大题,共计32分;立体几何两个小题,一个大题,共计22分解析几何两个小题,一个大题,共计22分;三角函数与解三角形两个小题,一个大题,共计20分;统计概率两个小题,一个大题,共计22分;数列一个小题,一个大题,共计17分;集合,复数与平面向量,各占5分。总体来看,数列比重有所增加。试卷整体上提升了对学生的数学运算和逻辑推理核心素养等的考查。二、试题坚持思想性与科学性的统一如新课标Ⅱ卷第3题,抽样了解学生参加体育运动的情况,第19题,要求合理平衡漏诊率和误诊率,制定检测标准,试题情境既有现实意义,也能很好地体现数学学科的应用价值。全面贯彻党的教育方针,落实立德树人根本任务,促进学生德智体美劳全面发展;反映新时代基础教育课程理念,落实考试评价改革、高中育人方式改革等相关要求.三、试题依据课程标准命题,深化基础考查如新课标Ⅱ卷第11题,其本质是根据一元二次方程根的性质判定方程系数之间的关系,题中函数经过求导以后,其既有极大值又有极小值的性质可以转化为一元二次方程有两个正根。深入考查直观想象素养,如新课标Ⅱ卷第9题以多选题的形式考查圆锥的内容,题目全面考查基础,四个选项设问逐次递进,前面的选项为后面的选项提供了条件,各选项分别考查圆锥的不同性质,互相联系,重点突出。扎实考查数学运算素养,要求考生理解运算对象,掌握运算法则,探究运算思路,求得运算结果。如新课标Ⅱ卷第10题设置了直线与抛物线相交的情境,通过直线方程与抛物线方程的联立考查计算能力。四.试题突出素养和能力考查,甄别思维品质如新课标Ⅱ卷第22题将导数与三角函数巧妙的结合起来,通过对导函数的分析,考查函数的单调性、极值等相关问题,通过导数、函数不等式等知识,深入考查了分类讨论的思想,化归与转化的思2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司想。如新课标Ⅱ卷第15题是一道开放题,有多个答案,考查直线与圆的位置关系、点到直线距离及圆内接三角形性质等知识内容。3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司题号分值题型考查内容命题点15单项选择复数复数的运算及几何意义25单项选择集合集合的包含...