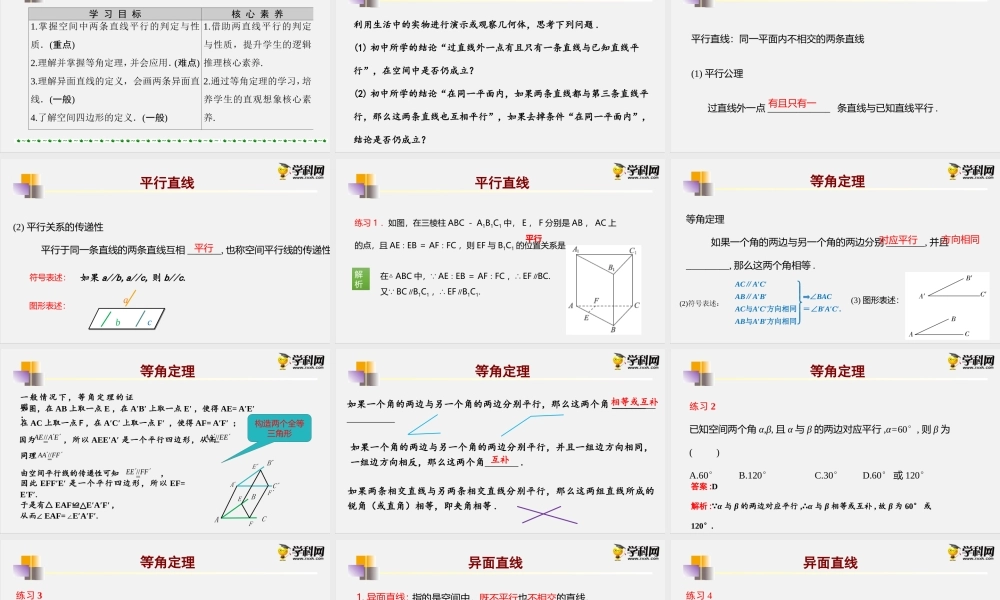
数学(人教B版2019)必修第四册11.3空间中的平行关系11.3.1平行直线与异面直线第十一章立体几何初步学习目标学习目标核心素养1.掌握空间中两条直线平行的判定与性质.(重点)2.理解并掌握等角定理,并会应用.(难点)3.理解异面直线的定义,会画两条异面直线.(一般)4.了解空间四边形的定义.(一般)1.借助两直线平行的判定与性质,提升学生的逻辑推理核心素养.2.通过等角定理的学习,培养学生的直观想象核心素养.尝试发现利用生活中的实物进行演示或观察几何体,思考下列问题.(1)初中所学的结论“过直线外一点有且只有一条直线与已知直线平行”,在空间中是否仍成立?(2)初中所学的结论“在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行”,如果去掉条件“在同一平面内”,结论是否仍成立?平行直线平行直线:同一平面内不相交的两条直线(1)平行公理过直线外一点_____________条直线与已知直线平行.有且只有一(2)平行关系的传递性平行于同一条直线的两条直线互相_______,也称空间平行线的传递性平行直线图形表述:如果a//b,a//c,则b//c.符号表述:abc平行解析练习1.如图,在三棱柱ABC-A1B1C1中,E,F分别是AB,AC上的点,且AE∶EB=AF∶FC,则EF与B1C1的位置关系是______.在△ABC中, AE∶EB=AF∶FC,∴EF∥BC.又 BC∥B1C1,∴EF∥B1C1.平行平行直线等角定理等角定理如果一个角的两边与另一个角的两边分别________,并且_________,那么这两个角相等.(2)符号表述:AC∥A′C′AB∥A′B′AC与A′C′方向相同AB与A′B′方向相同⇒∠BAC=∠B′A′C′.(3)图形表述:对应平行方向相同等角定理一般情况下,等角定理的证明.如图,在AB上取一点E,在A′B′上取一点E′,使得AE=A′E′;在AC上取一点F,在A′C′上取一点F′,使得AF=A′F′;因为,所以AEE′A′是一个平行四边形,从而.EAAE//EEAA//FFAA//同理由空间平行线的传递性可知,因此EFF′E′是一个平行四边形,所以EF=E′F′.FFEE//于是有△EAF≌△E′A′F′,从而∠EAF=E′A′F′∠.ABCABCEFEF构造两个全等三角形等角定理如果一个角的两边与另一个角的两边分别平行,那么这两个角_______相等或互补如果一个角的两边与另一个角的两边分别平行,并且一组边方向相同,一组边方向相反,那么这两个角.互补如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等,即夹角相等.等角定理练习2已知空间两个角α...