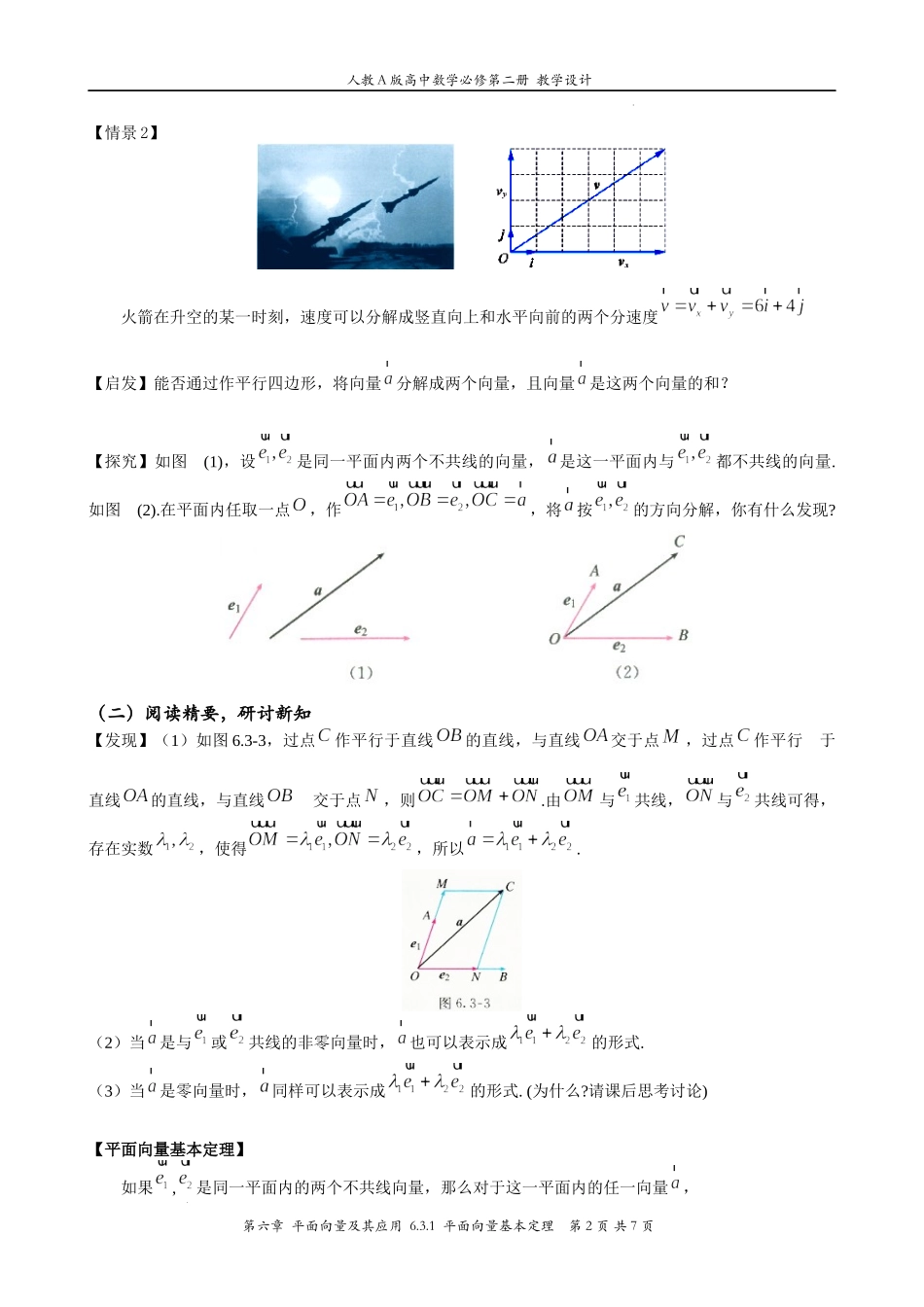
人教A版高中数学必修第二册教学设计第六章平面向量及其应用6.3.1平面向量基本定理第1页共7页学科网(北京)股份有限公司第六章平面向量及其应用6.3平面向量基本定理及坐标表示6.3.1平面向量基本定理一、教学目标1.了解平面向量基本定理及其意义;2.理解平面里的任何一个向量都可以用两个不共线的向量来表示,初步掌握应用向量解决实际问题的重要思想方法;3.能够在具体问题中适当地选取基底,其他向量能够用基底来表达.二、教学重点、难点教学重点:平面向量坐标表示的定理.教学难点:平面向量基本定理和应用.突破办法:渗透从特殊到一般的归纳,由“形”到“数”的数形结合的思想.三、学法与教学用具1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.2、教学用具:多媒体设备等四、教学过程(一)创设情景,揭示课题【复习回顾】1.实数与向量的积:实数与向量的积是一个向量,记作:(1);(2)时与方向相同;时与方向相反;时2.运算定律结合律:;分配律:;3.向量共线定理向量与非零向量共线的充要条件是:有且只有一个非零实数,使.【情景1】已知两个力,可以求出它们的合力,反过来,一个力可以分解为两个力,通过作平行四边形,将力F分解为多组大小、方向不同的分力.人教A版高中数学必修第二册教学设计第六章平面向量及其应用6.3.1平面向量基本定理第2页共7页学科网(北京)股份有限公司【情景2】火箭在升空的某一时刻,速度可以分解成竖直向上和水平向前的两个分速度【启发】能否通过作平行四边形,将向量分解成两个向量,且向量是这两个向量的和?【探究】如图(1),设是同一平面内两个不共线的向量,是这一平面内与都不共线的向量.如图(2).在平面内任取一点,作,将按的方向分解,你有什么发现?(二)阅读精要,研讨新知【发现】(1)如图6.3-3,过点作平行于直线的直线,与直线交于点,过点作平行于直线的直线,与直线交于点,则.由与共线,与共线可得,存在实数,使得,所以.(2)当是与或共线的非零向量时,也可以表示成的形式.(3)当是零向量时,同样可以表示成的形式.(为什么?请课后思考讨论)【平面向量基本定理】如果,是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,人教A版高中数学必修第二册教学设计第六章平面向量及其应用6.3.1平面向量基本定理第3页共7页学科网(北京)股份有限公司有且只有一对实数,使.【基底】若不共线,则称,为表示这一平面...