6.3.1 平面向量基本定理 课件-2021-2022学年高一下学期数学人教A版（2019）必修第二册.pptxVIP免费

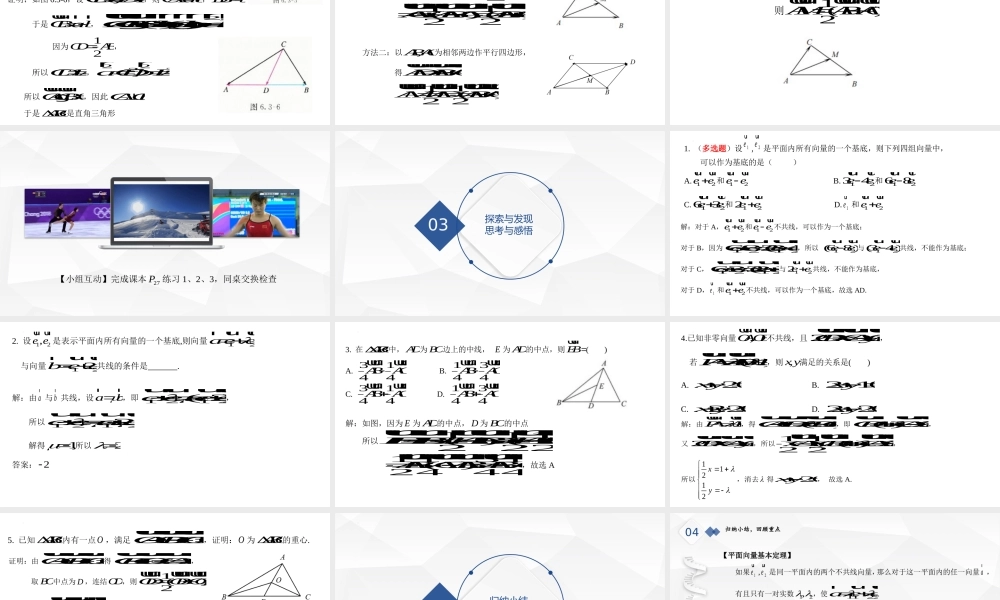
6.3.1平面向量基本定理第六章平面向量及其应用January26,2025创设情景揭示课题01【复习回顾】1．实数与向量的积：实数与向量ar的积是一个向量，记作：ar（1）||||||aarr；（2）0时ar与ar方向相同；0时ar与ar方向相反；0时0arr2．运算定律结合律：()()aarr；分配律：()aaarrr；()ababrrrr3.向量共线定理向量br与非零向量ar共线的充要条件是：有且只有一个非零实数，使barr.【情景1】已知两个力，可以求出它们的合力，反过来，一个力可以分解为两个力，通过作平行四边形，将力F分解为多组大小、方向不同的分力.【情景2】火箭在升空的某一时刻，速度可以分解成竖直向上和水平向前的两个分速度64xyvvvijrururrr【启发】能否通过作平行四边形，将向量ar分解成两个向量，且向量ar是这两个向量的和？【探究】如图(1)，设12,eeurur是同一平面内两个不共线的向量，ar是这一平面内与12,eeurur都不共线的向量.如图(2).在平面内任取一点O，作12,,OAeOBeOCauururuuururuuurr，将ar按12,eeurur的方向分解，你有什么发现?阅读精要研讨新知02【发现】（1）如图6.3-3，过点C作平行于直线OB的直线，与直线OA交于点M，过点C作平行于直线OA的直线，与直线OB交于点N，则OCOMONuuuruuuruuur.由OMuuur与1eur共线，ONuuur与2eur共线可得，存在实数12,，使得1122,OMeONeuuururuuurur，所以1122aeerurur.（2）当ar是与1eur或2eur共线的非零向量时，ar也可以表示成1122eeurur的形式.（3）当ar是零向量时，ar同样可以表示成1122eeurur的形式.(为什么?请课后思考讨论)【平面向量基本定理】如果1eur,2eur是同一平面内的两个不共线向量，那么对于这一平面内的任一向量ar，有且只有一对实数12,，使1122aeerurur.【基底】若12,eeurur不共线，则称1eur,2eur为表示这一平面内所有向量的一个基底．．.例题讨研【例题研讨】阅读领悟课本26P例1、例2例1如图6.3-4，，,OAOBuuruuur不共线，且()APtABtRuuuruuur，用,OAOBuuruuur表示OPuuur.解：因为,APtABABOBOAuuuruuuruuuruuuruur所以()OPOAAPOAtABOAtOBOAuuuruuruuuruuruuuruuruuuruur(1)tOAtOBuuruuur证明：如图6.3-6，设,CDaDAbuuurruuurr，则CAabuurrr，DBbuuurr于是CBabuurrr，22()()CACBabababuuruurrrrrrrgg因为12CDAB，所以C...