5.4.1正弦函数、余弦函数的图象（同步课件）-【一堂好课】2021-2022学年高一数学上学期同步精品课堂（人教A版2019必修第一册）.pptVIP免费

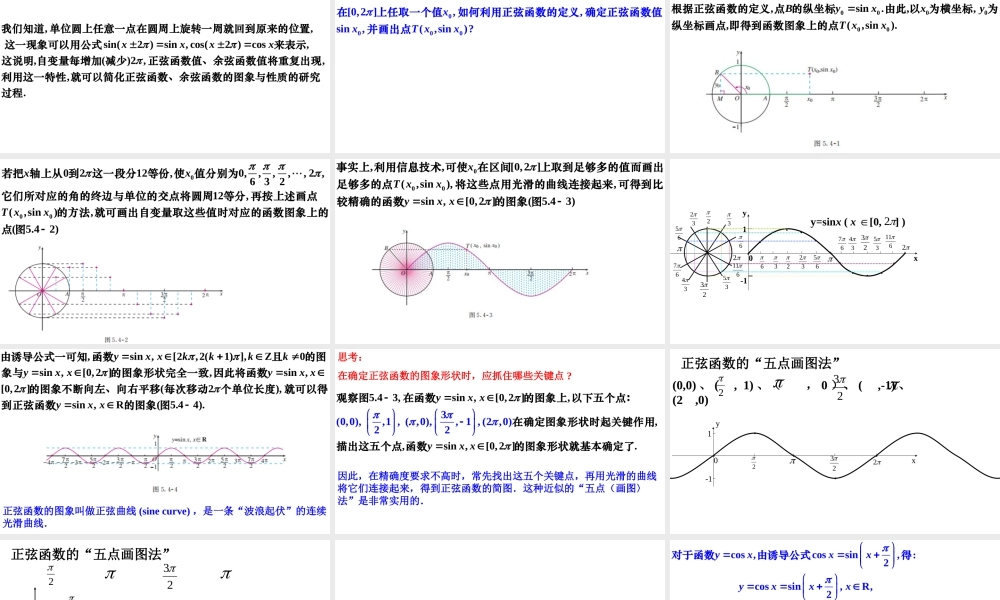
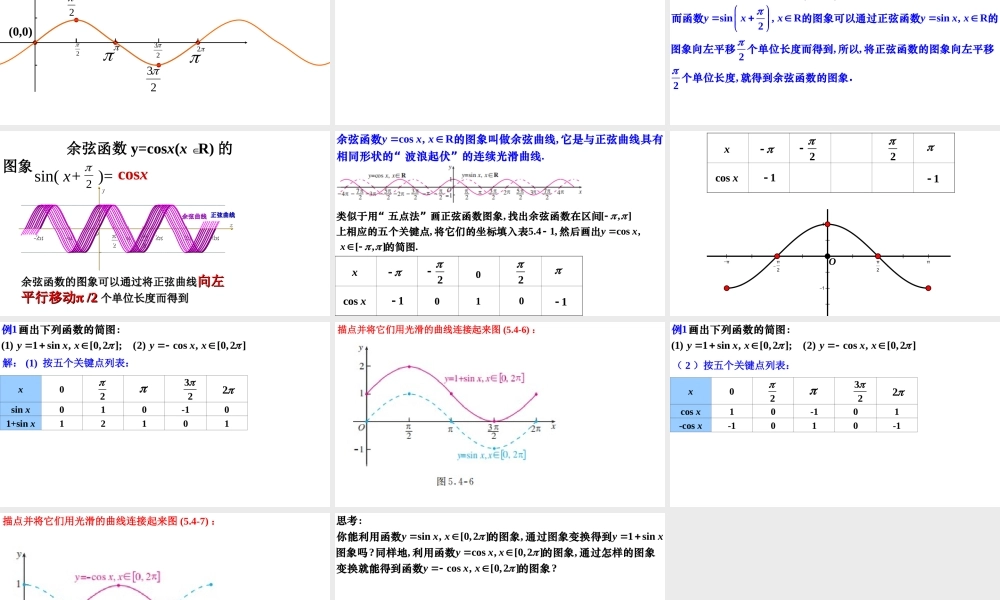
第五章三角函数人教A版2019必修第一册5.4三角函数的图象和性质5.4.1正弦函数、余弦函数的图象前面给出了三角函数的定义，如何从定义出发研究这个函数呢?类比已有的研究方法，可以先画出函数图象，通过观察图象的特征，获得函数性质的一些结论．sin(2)sin,cos(2)cos,,(2,,,,),.xxxx来表我们知道单位圆上任意一点在圆周上旋转一周就回到原来的位置这一现象可以用公式自变量每增加减少正弦函数值、余弦函数值将重复出现利用这一特性就可以简化正弦函数、余弦函数的图象与性质的研这说明究过程示sin,R,sin,[0,2].yxxyxx的图象从画函下面先数的图研究函象开始数0000[0,2],,sin,(,sin)?xxTxx在上任取一个值如何利用正弦函数的定义确定正弦函数值并画出点0000000(1,0).sin.,5.41,,,,,,,(,sin).OAOxBOxAyxxyTxBx如图在直角坐标系中画出以原点为与轴正半轴的交点为由此以为横坐标为纵坐标画点圆心的单位圆在单位圆上将点绕着点旋转弧度至点根据正弦函数的定义点的纵坐标即得到函数图象上的点0000212,0,,,,,2,632(,si12,5.42n),()xxTxx它们所对应的角的终边与单位的交点将圆周等分再按上述画点就可画出自变量取这些值时对应的函数图若把轴上从到这一段分等份使值分别为的方象上的点图法000,[0,2](,sin),sin,[0,2](,.43),5Txyxxxx利用信息技术可使在区间上取到足够多的值而画出足够多的点将这些点用光滑的曲线连接起事实上的图象来可得到比较精确的函数图1-1022322656723352yx●●●y=sinx(x[0,])∈2332346116633265●●●●●●●673435611●●●sin,[2,2(1)],Z0sin,[0,2]sin,[0,2](),sin,R(5.424),,.yxxkkkkyxxyxxyxx由诱导公式一可知函数的图象形状完全一致因此将函数的图象不断向左、向右平移每次移动个单位长度就可以得到正弦函数且的图象与的图象图正弦函数的图象叫做正弦曲线(sinecurve)，是一条“波浪起伏”的连续光滑曲线．思考：在确定正弦函数的图象形状时，应抓住哪些关键点?5.43,,,,3(0sin,[0,2]sin,[0,,0),,1,(,0),,21,(2,0)22.]yxxyxx观察图在函数的图象上以下五个点:在确定图象形状时起关键作用描出这五个点函数的图象形状就基本确定了因此，在精确度要求不高时，常先找出这五个关键点，再用光滑的曲线将它们连接起来，得到正弦函数的简图．...