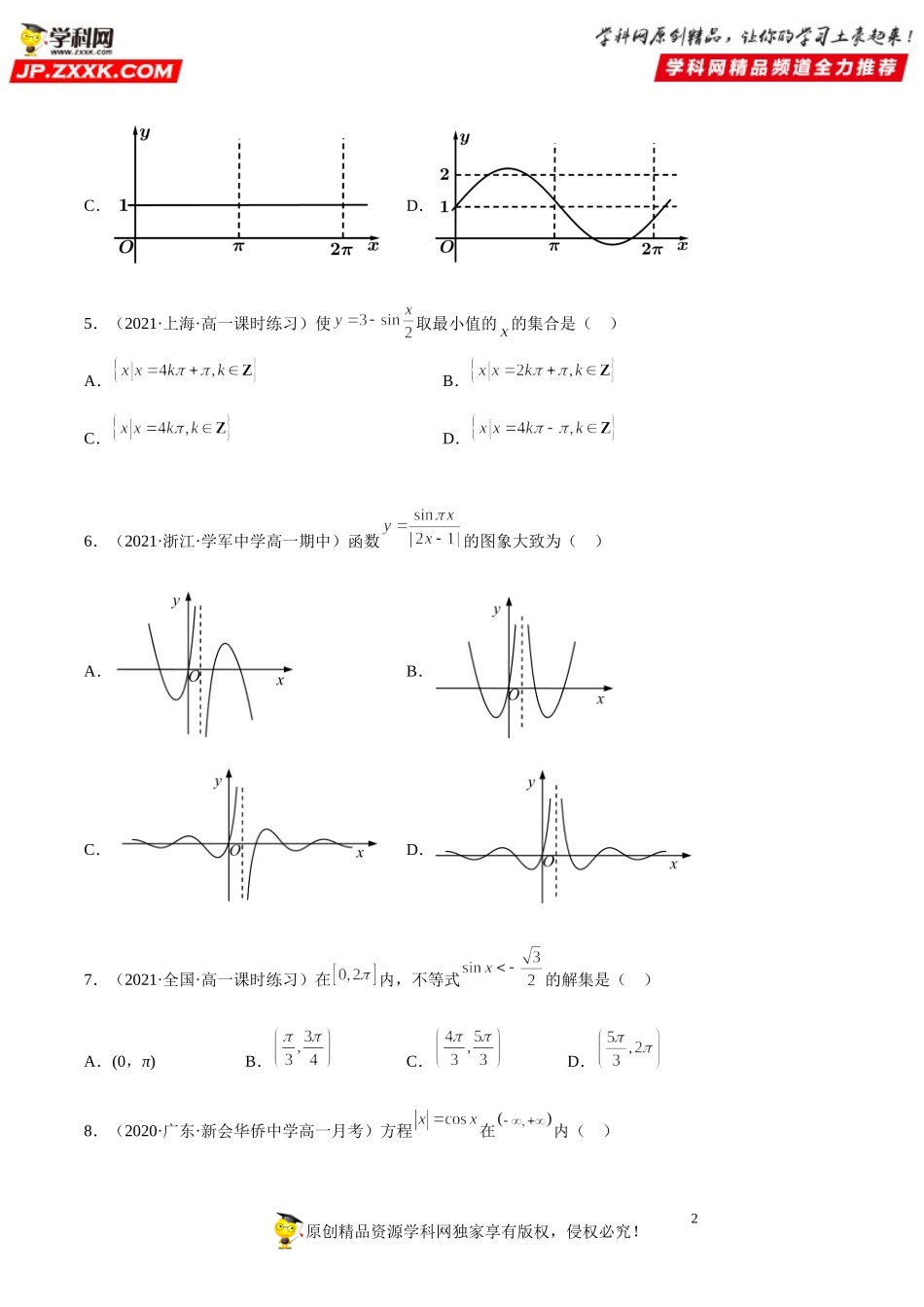
12021-2022学年高一数学【考题透析】满分计划系列(人教A版2019必修第一册)第五章三角函数5.4.1正弦函数、余弦函数的图象一、单选题1.(2021·全国·高一课时练习)函数的零点的个数为().A.3B.4C.5D.62.(2021·广西·全州县第二中学高一期中)使得正确的一个区间是()A.B.C.D.3.(2021·全国·高一单元测试)设函数,在区间上至少有2个不同的零点,至多有3个不同的零点,则的取值范围是()A.B.C.D.4.(2021·全国·高一单元测试)已知是实数,则函数的图象不可能是()A.B.原创精品资源学科网独家享有版权,侵权必究!2C.D.5.(2021·上海·高一课时练习)使取最小值的的集合是()A.B.C.D.6.(2021·浙江·学军中学高一期中)函数的图象大致为()A.B.C.D.7.(2021·全国·高一课时练习)在内,不等式的解集是()A.(0,π)B.C.D.8.(2020·广东·新会华侨中学高一月考)方程在内()原创精品资源学科网独家享有版权,侵权必究!3A.没有根B.有且仅有一个根C.有无穷多个根D.有且仅有两个根9.(2021·全国·高一课时练习)拱桥指的是在竖直平面内以拱作为结构主要承重构件的桥梁.如图是某拱桥的平面简化图,其形状可近似看作余弦型函数一个周期的图象,则其解析式可能是()A.B.C.D.10.(2020·广东·执信中学高一期末)若函数图像上存在不同的两点A,B关于y轴对称,则称点对是函数的一对“和谐点对”(注:点对与点对可看作同一对“和谐点对”.已知函数,则此函数的“和谐点对”有()A.0对B.1对C.2对D.3对11.(2021·上海·高一课时练习)关于函数y=sin|2x|,下列说法正确的是()A.周期为π,是奇函数B.值域为,关于对称C.在上递增,是偶函数D.是非奇非偶函数,函数最大值为212.(2021·甘肃·嘉峪关市第一中学高一期中)已知定义在区间的函数,则函数的解集是()A.B.C.D.二、多选题原创精品资源学科网独家享有版权,侵权必究!413.(2021·全国·高一课时练习)函数的图象与直线的交点个数可能是()A.0B.1C.2D.314.(2020·全国·高一课时练习)下列在(0,2π)上的区间能使cosx>sinx成立的是()A.B.C.D.∪15.(2020·全国·高一课时练习)若函数()的图象和直线围成一个封闭的平面图形,则下列说法正确的是()A.当(,)时,B.C.D.阴影部分的面积为16.(2021·上海·高一单元测试)已知a是实数,则函数的图像可能是()A.B.C.D.17.(2021·海南·高一...