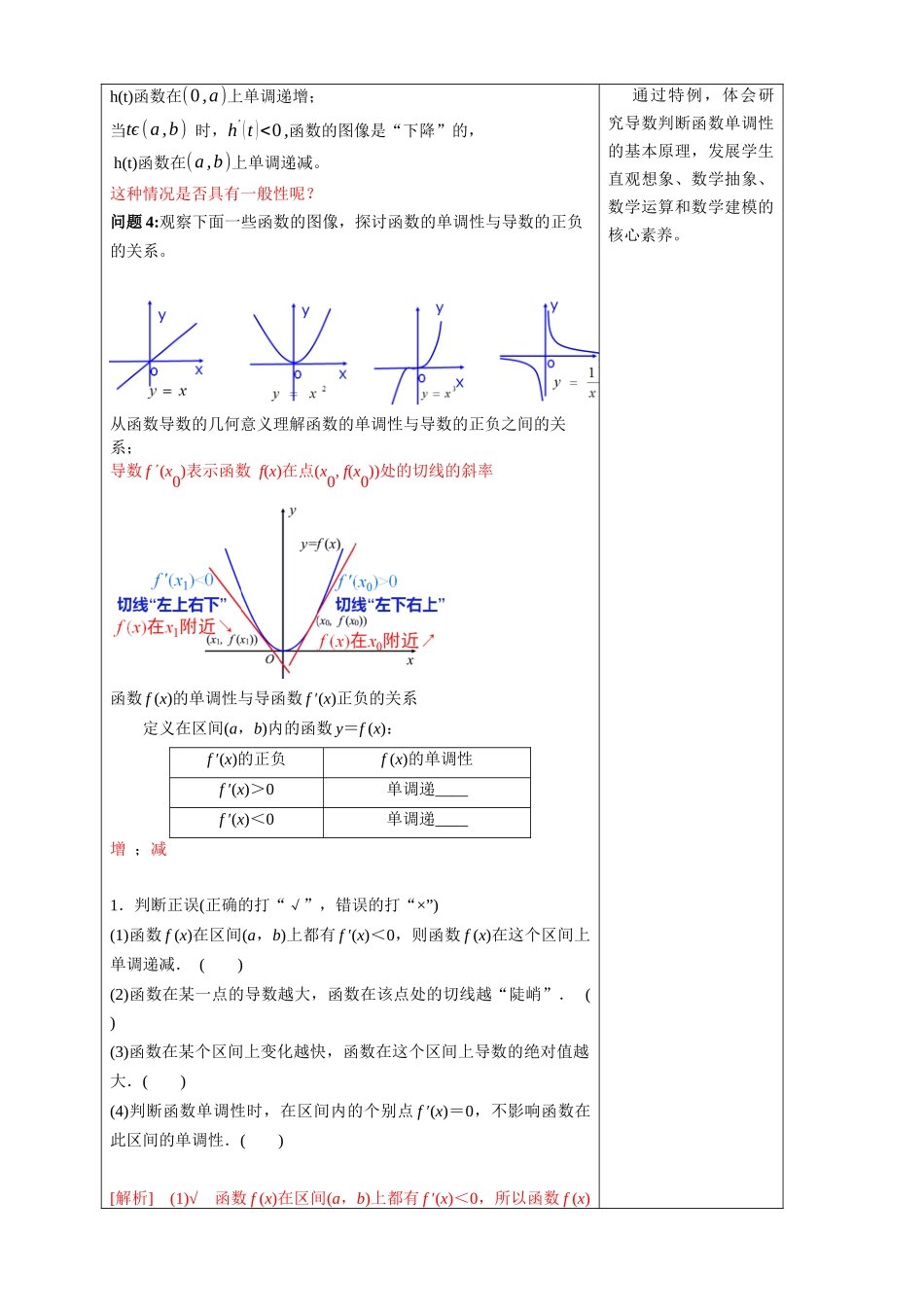
5.3.1函数的单调性(一)教学内容函数的单调性(二)教材分析函数的单调性是函数性质中的一个重要性质,学生在必修一中已经学习了函数单调性的内容,如利用函数图像、单调性定义来研究函数的单调性,在学习导数的基础上利用导数相关知识研究函数单调性是导数的一个重要应用,也为下一节学习函数的极值打下基础,因此,本节内容具有承上启下的作用。(三)学情分析1.认知基础:学习函数单调性。(四)教学目标1.知识目标:通过具体函数图象,发现函数的单调性与导数的正负之间的关系,体会数形结合思想,发展直观想象素养。2、能力目标:能根据函数导数的正负判断函数的单调性,体会算法思想,发展数学运算素养。3、素养目标:1.数学抽象:导数正负与函数单调性关系2.逻辑推理:运用导数正负判断函数单调性3.数学运算:函数单调区间的求解4.直观想象:导数与函数单调性的关系(五)教学重难点重点:理解函数的单调性与导数的正负之间的关系难点:运用导数判断函数的单调性(六)教学思路与方法(七)课前准备(八)教学过程一、新知探究在必修第一册中,我们通过图像直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等的性质。在本章前两节中我们学习了导数的概念和运算,知道导数是关于瞬时变化率的数学表达,它定量地刻画了函数的局部变化,能否利用导数更加精确地研究函数的性质呢?本节我们就来讨论这个问题。问题1:判断函数单调性的方法有哪些?1.定义法:2.图像法:3.性质法:增+增→增,减+减→减,增→减,复合函数单调性同增异减4.导数法问题2:图(1)是某高台跳水运动员的重心相对于水面的高度h随时间变化的函数h(t)=-4.9t2+4.8t+11图像.图(2)是跳水运动员的速度v随时间t的变化的函数v(t)=h'(t)=¿-9.8t+4.8的图象,a=2449,b是函数h(t)的零点。运动员从起跳到最高点,及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?观察图像可以发现(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)是单调递增,相应地,相应的v(t)=h'(t)>0(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度h随时间t的增加而减小,即h(t)是单调递减,相应地,v(t)=h'(t)<0问题3:我们看到,函数h(t)的单调性与h'(t)的正负有内在联系,那么,我们能否由h'(t)的正负来判断函数h(t)的单调性呢?对于高台跳水问题,可以发现:当tϵ(0,a)时,h'(t)>0,函数的...