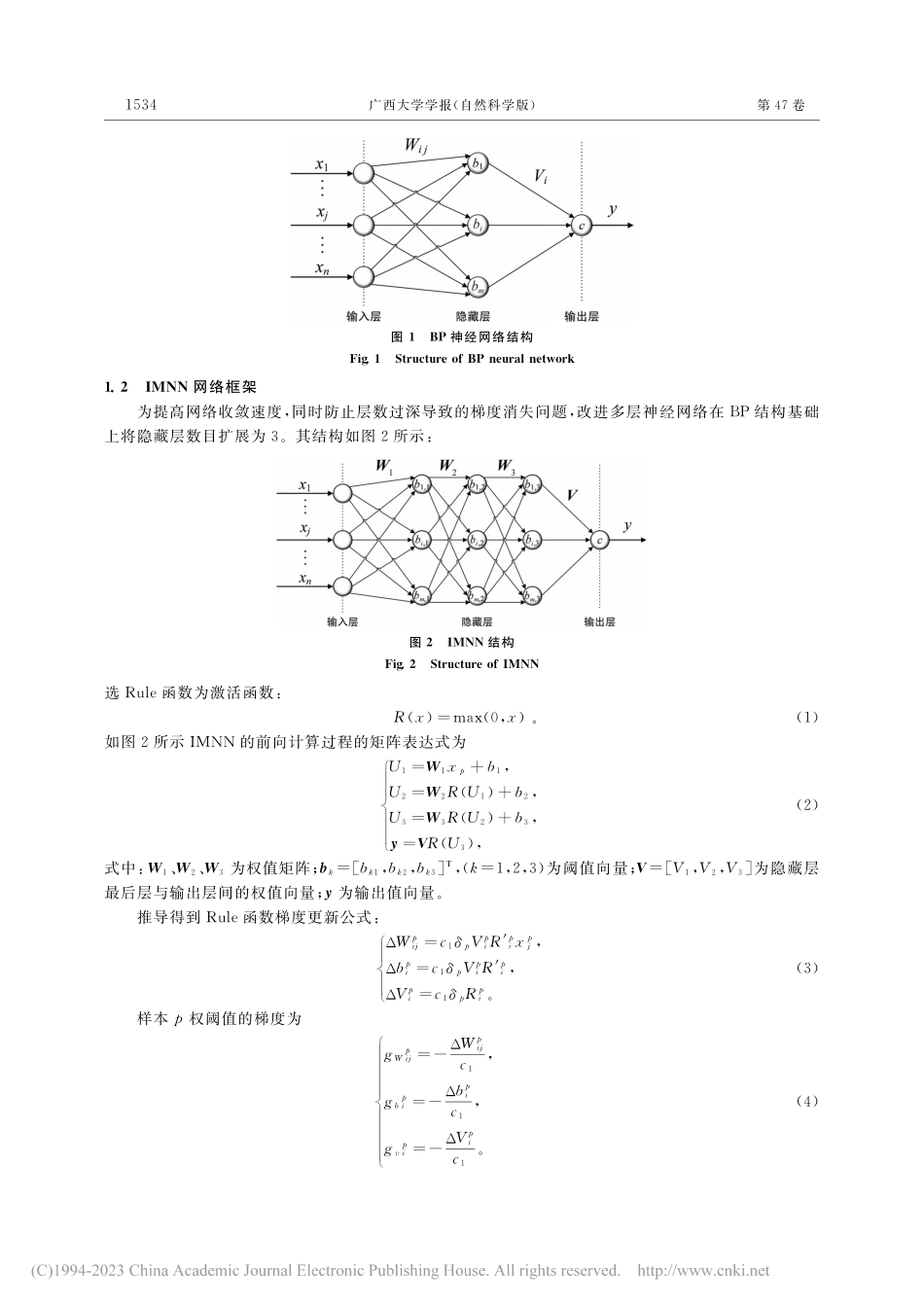
第47卷第6期2022年12月广西大学学报(自然科学版)JournalofGuangxiUniversity(NaturalScienceEdition)Vol.47No.6Dec.2022收稿日期:2022-05-18;修订日期:2022-09-28基金资助:国家自然科学基金项目(61861003);广西自然科学基金项目(2021GXNSFAA220136)通讯作者:孔繁镍(1973—),男,广西贵港人,广西大学教授,博士;E-mail:kongfannie@163.com。引文格式:陆文玲,夏家辉,孔繁镍.自适应反归一化改进多层神经网络轴流转桨水轮机协联功率预测[J].广西大学学报(自然科学版),2022,47(6):1532-1542.DOI:10.13624/j.cnki.issn.1001-7445.2022.1532自适应反归一化改进多层神经网络轴流转桨水轮机协联功率预测陆文玲1,夏家辉2,孔繁镍2*(1.南宁职业技术学院智能制造学院,广西南宁530008;2.广西大学电气工程学院,广西南宁530004)摘要:轴流转桨水轮机现场协联试验受经济和时间成本限制,获取的数据量有限,难以全面指导机组协联运行参数设置。为提高协联试验效率,实现水轮机协联工况下的功率追踪,同时避免水轮机物理模型高度非线性化难以模拟实际现场问题,提出一种基于改进多层神经网络数学预测模型,采用Rule函数、L2正则化、Adam优化器并用PSO算法优化其梯度参数。针对神经网络实际预测缺乏真实值的问题,提出自适应反归一化区间端值判断策略提高实际预测准确度。通过协联与非协联仿真分析,结果表明所提出预测模型和区间策略能够在小样本情况下对轴流转桨水轮机协联工况实现有效的实际预测,具有较高精度。关键词:轴流转桨水轮机;协联试验;多层神经网络预测模型;自适应反归一化中国分类号:TM312文献标识码:A文章编号:1001-7445(2022)06-1532-11Kaplanturbinecoordinationpowerpredictionbasedonimprovedmultilayerneuralnetworkwithadaptiveanti-normalizationLUWen-ling1,XIAJia-hui2,KONGFan-nie2*(1.SchoolofIntelligentManuf...