期末测试卷2.5 实验：用单摆测量重力加速度.docx

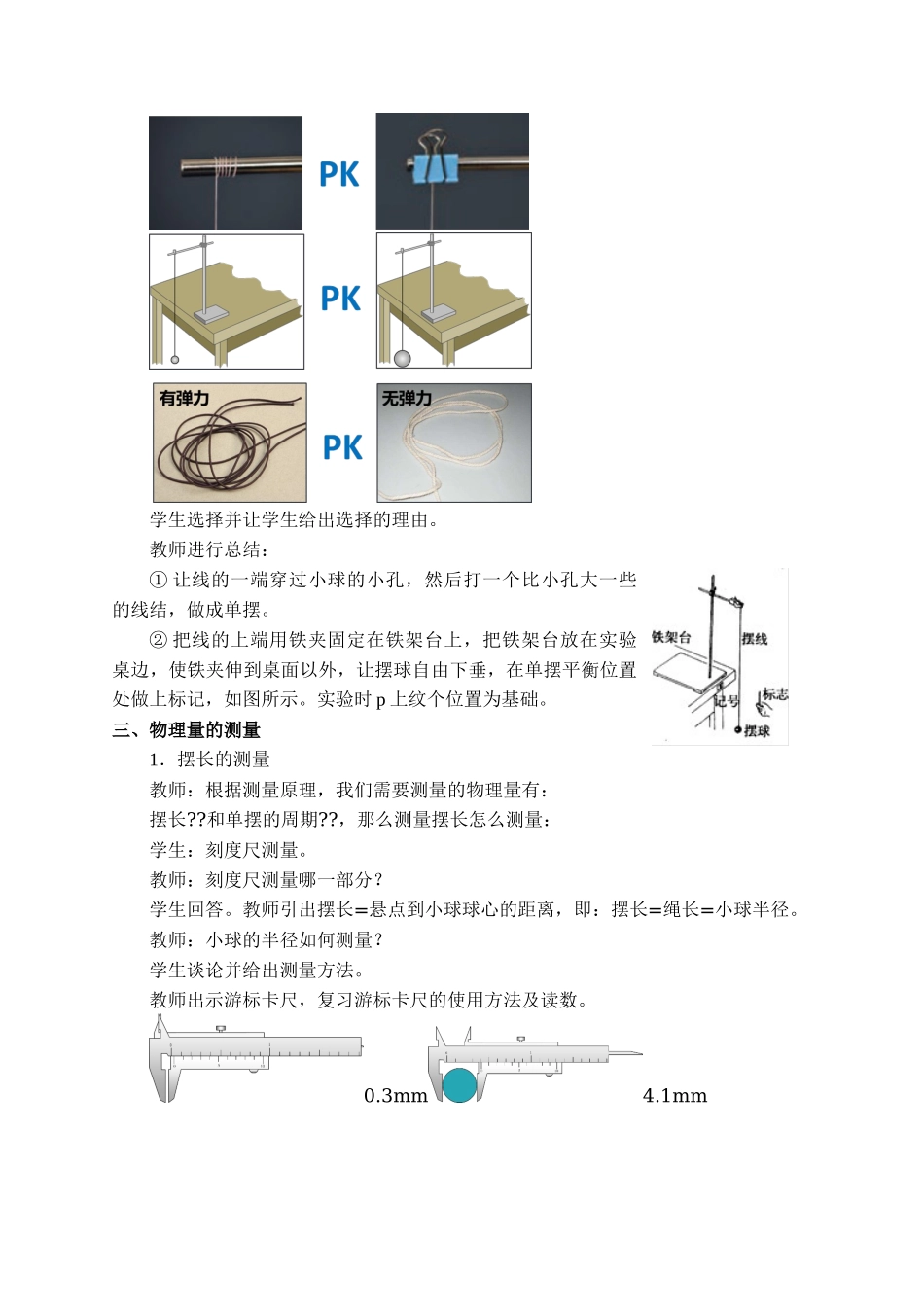
实验：用单摆测量重力加速度 【教学目标】 1．学会用单摆测定当地的重力加速度。 2．能正确使用秒表。 3．巩固和加深对单摆周期公式的理解。 4．学习用累积法减小相对误差的方法。 【教学重难点】 1．学会用单摆测定当地的重力加速度。 2．学习用累积法减小相对误差的方法。 【教学准备】 长约lm的细丝线一根，球心开有小孔的金属小球一个，带有铁夹的铁架台一个，毫米刻度尺一根，秒表一块，游标卡尺一把。 【教学过程】 一、实验思路 教师：上节课学习了单摆的相关知识，大家是否还记得单摆的周期公式？ 引导学生会顾单摆的周期公式以及试用条件 1．公式：T=2πlg 2．使用条件：（1）θ<5° （2）小球为质点（大小与绳长相比可以忽略不计） 教师：可以看出周期公式中含重力加速度g，那么我们可以根据测量单摆的周期来间接测量重力加速度的大小。 3．测量原理：g=4π2lT2 其中l为摆长，T为单摆的周期 由于一般单摆的周期都不长，例如摆长1m左右的单摆其周期约为2s。所以依靠人为的秒表计时产生的相对误差会很大。针对这一问题本实验采用累积法计时。即不是测定一个周期，而是测定几十个周期，例如30或50个周期。这样一来，人用秒表计时过程中产生的误差与几十个周期的总时间相比就微乎其微了。这种用累积法减小相对误差的方法在物理实验中经常会遇到，希望学生要认真领会其精神实质，为以后的应用打下基础。 二、实验装置 教师出示装置的对比图，让学生判断选择哪种装置。 学生选择并让学生给出选择的理由。 教师进行总结： ①让线的一端穿过小球的小孔，然后打一个比小孔大一些的线结，做成单摆。 ②把线的上端用铁夹固定在铁架台上，把铁架台放在实验桌边，使铁夹伸到桌面以外，让摆球自由下垂，在单摆平衡位置处做上标记，如图所示。实验时p上纹个位置为基础。 三、物理量的测量 1．摆长的测量 教师：根据测量原理，我们需要测量的物理量有： 摆长??和单摆的周期??，那么测量摆长怎么测量： 学生：刻度尺测量。 教师：刻度尺测量哪一部分？ 学生回答。教师引出摆长=悬点到小球球心的距离，即：摆长=绳长=小球半径。 教师：小球的半径如何测量？ 学生谈论并给出测量方法。 教师出示游标卡尺，复习游标卡尺的使用方法及读数。 0.3mm4.1mm 10.5mm10.90mm 10.24mm17.00mm 2．周期的测量 （1）回顾秒表的使用及读数方法： 2分7.6秒1分51.4秒 （2）单摆周期的测量方法： 引导学生回顾单摆的周期是什么？ 怎样测量单摆的周期比较准确？ 学生讨论，教师总结： 从摆球通过平衡位置开始记时，并且采用倒数到0开始记时计数的方法，即……4，3，2，1，0，在数到“零”的同时按下秒表开始记时计数。测量n个周期的总时间t，用t/n得到单摆的周期。 四、实验步骤 1．用米尺测出悬线长度L（准确到毫米），用游标卡尺测出摆球的直径D。 2．将摆球从平衡位置拉开一个很小角度（不超过5°），然后放开摆球，使摆球在竖直平面内摆动。 3．用秒表测出单摆完成30次或50次全振动的时间（注意记振动次数时，以摆线通过标记为准）。 4．计算出平均完成一次全振动所用的时间，这个时间就是单摆的振动周期。 5．改变摆长，重做几次实验，每次都要记录摆线长度L，振动次数以和振动总时间t。 6．根据单摆的周期公式，计算出每次实验的重力加速度，求出几次实验得到的重力加速度的平均值，即是本地区的重力加速度的平均值。 7．将测得的重力加速度数值与当地重力加速度数值加以比较，分析产生误差的可能原因。 【典型范例导析】 用单摆测定重力加速度的数据处理方法有哪些？试用自己的语言叙述误差来源及误差分析。 解析（1）数据处理方法 方法一（公式法） 根据公式g=4π2lT2可以计算出重力加速度的数值。 但在实际实验中上式应改写成g=4π2n2（L'+d2）t2（L’为摆线长度） gl=__________=_______，g2=__________=__________， g3=__________=__________，取平均值g=__________。 方法二（图象法） 作T2-L图象。由g=4π2lT2可以知道T2-L图象应是一条过原点的直线，其斜率k的物理意义是4π2g。所以作出T2-L图象后求斜率k（k=∆T2∆L），然后可求出重力加速度g=4π2k。 五、注意事项 1．选择细线时应选择细、轻而且不易伸长，长度约1米左右的细线，小球应选密度较大、半径较小的金属球。 2．单摆摆线的上端应夹紧，不能卷在铁夹的杆上，以免造成悬点不固定，摆长变化的现象。 3．测量摆长时应注意是悬点到球心的距离，等于摆线长加上小球半径。注意摆线长与摆长的区别。 4．要使单摆在竖直平面内摆动，不要形成圆锥摆。 5．要注意控制摆球的最大摆角不超过5°。 6．计算单摆的振动次数时，应从小球通过最低位置时开始计时，同方向再次通过最低位置时，计数为1、2……。 7．改变悬线长度多次测量，最后求出g的平均值。 六、误差分析 1．系统误差 主要来自于单摆模型本身是否符合要求，即悬点是否固定，摆球和摆长是否符合要求，最大摆角是否不超过5°，是否在同一竖直平面内摆动等。 2．偶然误差 （1）主要来自于时间测量，测量时间时要求从摆球通过平衡位置开始计时，在记次数时不能漏记或多记。同时应多次测量，再对多次测量结果求平均值。 （2）测长度和摆球直径时，读数也容易产生误差。秒表读数读到秒的十分位即可。 【例1】在用单摆测定重力加速度实验中： （1）为了比较准确地测量出当地的重力加速度值，应选用下列所给器材中的哪些？将你所选用的器材前的字母填在题后的横线上。 A．长1m左右的细绳；B．长30cm左右的细绳；C．直径2cm的铅球；D．直径2cm的铁球；E．秒表；F．时钟；G．最小刻度是厘米的直尺；H．最小刻度是毫米的直尺。 所选器材是____________________________________________________________。 （2）实验时对摆线偏离竖直线的要求是_____________________________________；理由是_____________________________________________________________________。 解析（1）所选器材为A、C、E、H。（2）偏角要求小于5°。 根据本实验的原理：振动的单摆，当摆角小于5°时，其振动周期与摆长的平方根成正比，与重力加速度的平方根成反比，而与偏角的大小（振幅）、摆球的质量无关，周期公式为T=2πlg。经变换得g=4π2lT2。因此，在实验中只要测出单摆的摆长L和振动周期T，就可以求出当地的重力加速度g的值，本实验的目的是测出g的值，而不是验证单摆的振动规律。如果在实验中选用较短的摆线，既会增大摆长的测量误差，又不易于保证偏角9小于5°摆线较长，摆角满足小于5°的要求，单摆的振动缓慢，方便记数和记时。所以应选A．摆球应尽量选重的，所以选C。 因为单摆振动周期丁的测量误差对重力加速度g的影响较大，所以计时工具应选精确度高一些的秒表。摆长的测量误差同样对g的影响较大，也应选精确度较高的最小刻度为毫米的直尺。 （2）因为当摆球振动时，球所受的回复力F=mgsinθ，只有当θ<5°时，sinθ≌θ此摆才称为单摆，其振动才是简谐振动，周期T=2πlg的关系式才成立。 【例2】在做“用单摆测定重力加速度”的实验时，用摆长L和周期T计算重力加速度的公式是g=_____。 如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图示，那么单摆摆长是_____。如果测定了40次全振动的时间如图中秒表所示，那么秒表读数是_____s。单摆的摆动周期是_____s。 解析这是一道考查考生观察能力和刻度尺及秒表的读数方法的考题。关于秒表的读数问题，上海市的高考题中不只一次出现过，但是学生仍不会读，主要原因是不清楚分钟（短针）和秒钟（长针）之间的关系。因此此题仍具有较强的考查功能。 本题答案为：T=2πLg，0.8740m或87.40cm，75.2s，1.88s。单摆的摆长应等于测量值88.40cm减去摆球的半径lcm，得到87.40cm。 【例3】某同学在用单摆测定重力加速度的实验中，测量5种不同摆长情况下单摆的振动周期，记录表格如下： 以L为横坐标，T2为纵坐标，作出T2-L图象：并利用此图线求重力加速度。 解析：由单摆周期公式T=2πLg得T2=4π2Lg，所以T2-L图线是过坐标原点的一条直线，直线斜率是k=4π2g。因此，g=4π2k，作出图象如图所示，求得直线斜率为k=4.00，即g=4π2k=9.86（m/s2） 【跟踪训练】 1．某同学在做利用单摆测定重力加速度实验中，如果测得的g值偏小，可能原因是（ ） A．测摆线长时摆线拉得过紧 B．摆线上端悬点未固定，振动中出现松动使摆线长度增加了 C．开始记时时，秒表按下时刻滞后于单摆振动的记数 D．实验中误将49次全振动记为50次全振动 2．一位同学用单摆做测量重力加速度实验，他将摆挂起后，进行了如下步骤： A．测摆长L：用米尺量出摆线的长度； B．测周期T：将摆球拉起，然后放开，在摆球某次通过最低点时，按下秒表开始记时，同时将此次通过最低点作为第1次，接着一直数到摆球第60次通过最低点时，按下秒表停止记时，读出这段时间t，算出单摆的周期T=t/60； C．将所测得的L和T代人单摆的周期公式T=2πLg，算出g，将它作为实验的最后结果写入实验报告中去。（不要求进行误差计算）。 上述步骤中错误或遗漏的步骤有________，应改正为________________________。 3．用单摆测定重力加速度实验中，得到如下一组有关数据： （1）利用上述数据在图中描出图线 （2）利用图线，取4π2=39.5，则重力加速度大小为________。 （3）在实验中，若测得g值偏小，可能是下列原因中的（ ） A．计算摆长时，只考虑悬线长度，而未加小球半径 B．测量周期时，将九次全振动误记为n+1次全振动 C．计算摆长时，将悬线长加小球直径 D．单摆振动时，振幅偏小 4．在用单摆测重力加速度实验中，操作时，必须注意下面的问题。请在横线上填上题设中的关键问题。 A．摆球要选用密度较________而直径较________的小球。摆线要选取较________。且线径较________和不易伸长的线。 B．在固定摆线上端时应用铁夹夹紧，不要缠绕，悬点要固定不变，以免在摆动过程中________发生变化。 C．摆长是从________到________的距离，测量时要尽量准确。 D．实验时必须控制摆角在________以内，并且要让单摆在________内摆动。 E．测量单摆周期时，等单摆自由振动几次之后，从摆球经过________位置开始记时，因为这时摆球的速度________，容易观察，可以减小误差。 5．图中是一只秒表，这只秒表最小分度是________，最大计时是________。此表所记录的时间示数为________。 6．在做“用单摆测定重力加速度”的实验时，用摆长L和周期T计算重力加速度的公式是g=________。某同学做此实验时，测得摆球直径为16.0mm，用米尺测量摆长，结果如图所示。测量单摆完成38次全振动的时间的秒表读数如图所示，则摆长L=________cm，秒表读数为________s，当地重力加速度为g=________m/s2（保留三位有效数字）。 【答案与提示】 1．B（根据g=4π2LT2知，g偏小可能原来是L的测量值偏小或T的测量值偏大。选项A中摆线拉得过紧，使L变大，因此测得g偏大；选项B中，在摆长已测定情况下，由于悬点松动使摆长增加，实际振动的摆长大于测量值，所以测量值也偏小。选项C和D均为测得的周期偏小，故g值偏大。） 2．A、B、C三处均有遗漏和错误的地方。A改正为：要用游标卡尺测摆球的直径d，摆长L=摆线长（l）+摆球半径（d/2）（或用米尺测量摆长时应取悬点至球心的距离）。B改正为：T=t/29.5。C改正为：应多次测量，然后取平均值，将平均值的g作为实验的最后结果。这里所要考查的是学生是否会正确测量摆长和周期，尤其是要理解多次测量、取平均值的实际意义。 3．（1）如图 （2）9.875m/s2（由图可知，只有第1次测量数据偏离直线较远，也说明摆长太短，测量误差较大。从第2次至第5次的结果均在图线上。△T2=（4.8-2.4）s2=2.4s2，△L=（1.2-0.6）m=0.6m，k'=∆L∆T2，根据例3知，在T2-L图象中，g=4π2k，k为图线的斜率，且k=∆T2∆L，此处k'=1k，所以g=4πk'=4π∆L∆T2=39.5×0.62.4m/s2=9.875m/s2。 （3）A（根据g=4π2LT2知，只有选项A的情况使g值偏小，其余都偏大。） 4． A．大、小、长、细； B．摆长发生变化； C．摆线悬点，摆球球心； D．5°，竖直平面（防止摆球做圆锥摆运动）； E．平衡位置，最大。 5．0.1 s，15min，3’42"2 6．4π2LT2，0.990，75.2，9.95