迈克耳孙干涉仪··.doc

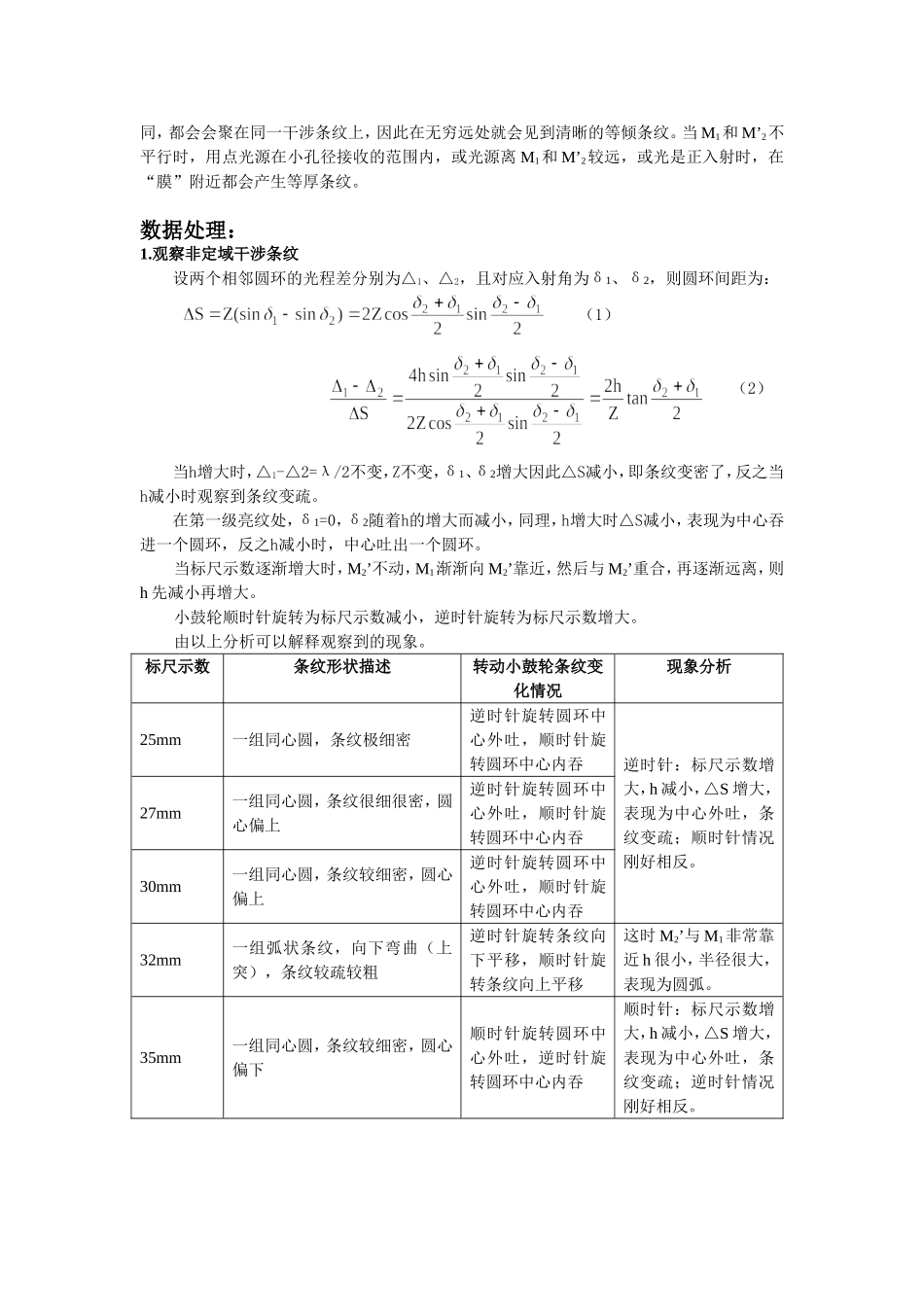
实验题目：迈克尔孙干涉仪 实验目的： 了解迈克尔孙干涉仪的原理、结构和调节方法，观察非定域和定域干涉条纹，测量氦氖激光的波长，并增强对条纹可见度和时间相干性的认识。 实验原理： 1． 迈克尔孙干涉仪的结构和原理 迈克尔孙干涉仪的原理图如图3.1.1-1所示，A和B为材料、厚度完全相同的平行板，A的一面镀上半反射膜，M1、M2为平面反射镜，M2是固定的，M1和精密丝杆相连，使其可前后移动，最小读数为10-4mm，可估计到10-5mm，M1和M2后各有几个小螺丝可调节其方位。 光源S发出的光射向A板而分成（1）、（2）两束光，这两束光又经M1和M2反射，分别通过A的两表面射向观察处O，相遇而发生干涉，B作为补偿板的作用是使（1）、（2）两束光的光程差仅由M1、M2与A板的距离决定。 由此可见，这种装置使相干的两束光在相遇之前走过的路程相当长，而且其路径是互相垂直的，分的很开，这正是它的主要优点之一。从O处向A处观察，除看到M1镜外，还可通过A的半反射膜看到M2的虚像M’2，M1与M2镜所引起的干涉，显然与M1、M’2引起的干涉等效，M1和M’2形成了空气“薄膜”，因M’2不是实物，故可方便地改变薄膜的厚度（即M1和M’2的距离），甚至可以使M1和M’2重叠和相交，在某一镜面前还可根据需要放置其他被研究的物体，这些都为其广泛的应用提供了方便。 2． 点光源产生的非定域干涉 一个点光源S发出的光束经干涉仪的等效薄膜表面M1和M’2反射后，相当于由两个虚光源S1、S2发出的相干光束（图3.1.1-2）。若原来空气膜厚度（即M1和M’2之间的距离）为h，则两个虚光源S1和S2之间的距离为2h，显然只要M1和M’2（即M2）足够大，在点光源同侧的任一点P上，总能有S1和S2的相干光线相交，从而在P点处可观察到干涉现象，因而这种干涉是非定域的。 若P点在某一条纹上，则由S1和S2到达该条纹任意点（包括P点）的光程差是一个常量，故P点所在的曲面是旋转双曲面，旋转轴是S1、S2的连线，显然，干涉图样的形状和观察屏的位置有关。当观察屏垂直于S1、S2的连线时，干涉图是一组同心圆。下面我们利用图3.1.1-3推导的具体形式。光程差 把小括号内展开，则 由于h<<Z，所以 （1） 从式（1）可以看出，在δ=0处，即干涉环的中心处光程差有极大值，即中心处干涉级次最高。如果中心处是亮的，则。若改变光程差，使中心处仍是亮的，则，我们得到 （2） 即M1和M2之间的距离每改变半个波长，其中心就“生出”或“消失”一个圆环。两平面反射镜之间的距离增大时，中心就“吐出”一个个圆环。反之，距离减小时中心就“吞进”一个个圆环，同时条纹之间的间隔（即条纹的稀疏）也发生变化。由式（2）可知，只要读出干涉仪中M1移动的距离h和数出相应吞进（或吐出）的环数就可求得波长。 把点光源换成扩展光源，扩展光源中各点光源是独立的、互不相干的，每个点光源都有自己的一套干涉条纹，在无穷远处，扩展光源上任两个独立光源发出的光线，只要入射角相同，都会会聚在同一干涉条纹上，因此在无穷远处就会见到清晰的等倾条纹。当M1和M’2不平行时，用点光源在小孔径接收的范围内，或光源离M1和M’2较远，或光是正入射时，在“膜”附近都会产生等厚条纹。 数据处理： 1.观察非定域干涉条纹 设两个相邻圆环的光程差分别为△1、△2，且对应入射角为δ1、δ2，则圆环间距为： （1） （2） 当h增大时，△1-△2=λ/2不变，Z不变，δ1、δ2增大因此△S减小，即条纹变密了，反之当h减小时观察到条纹变疏。 在第一级亮纹处，δ1=0，δ2随着h的增大而减小，同理，h增大时△S减小，表现为中心吞进一个圆环，反之h减小时，中心吐出一个圆环。 当标尺示数逐渐增大时，M2’不动，M1渐渐向M2’靠近，然后与M2’重合，再逐渐远离，则h先减小再增大。 小鼓轮顺时针旋转为标尺示数减小，逆时针旋转为标尺示数增大。 由以上分析可以解释观察到的现象。 标尺示数 条纹形状描述 转动小鼓轮条纹变化情况 现象分析 25mm 一组同心圆，条纹极细密 逆时针旋转圆环中心外吐，顺时针旋转圆环中心内吞 逆时针：标尺示数增大，h减小，△S增大，表现为中心外吐，条纹变疏；顺时针情况刚好相反。 27mm 一组同心圆，条纹很细很密，圆心偏上 逆时针旋转圆环中心外吐，顺时针旋转圆环中心内吞 30mm 一组同心圆，条纹较细密，圆心偏上 逆时针旋转圆环中心外吐，顺时针旋转圆环中心内吞 32mm 一组弧状条纹，向下弯曲（上突），条纹较疏较粗 逆时针旋转条纹向下平移，顺时针旋转条纹向上平移 这时M2’与M1非常靠近h很小，半径很大，表现为圆弧。 35mm 一组同心圆，条纹较细密，圆心偏下 顺时针旋转圆环中心外吐，逆时针旋转圆环中心内吞 顺时针：标尺示数增大，h减小，△S增大，表现为中心外吐，条纹变疏；逆时针情况刚好相反。 2.测量氦氖激光的波长 n 0 50 100 150 200 h(mm) 35.16000 35.17723 35.19308 35.20918 35.22511 n 250 300 350 400 450 h(mm) 35.24182 35.25795 35.27405 35.29033 35.30675 根据数据作h~n图像，并线性拟和得到 Linear Regression for Data1_B: Y = A + B * X Parameter Value Error ------------------------------------------------------------ A 35.16045 1.68977E-4 B 3.24887E-4 6.33044E-7 ------------------------------------------------------------ R SD N P ------------------------------------------------------------ 0.99998 2.87495E-4 10 <0.0001 ------------------------------------------------------------ 因此回归方程为Δh=35.16045+3.24887*10-4n 斜率k=3.24887*10-4mm=324.887nm 相关系数r=0.99998 斜率的标准差mm=0.633044nm λ=2Δh/n=2k=649.774nm UA(λ)=2sk=1.267nm 波长的测量结果为 λ=(649.774±1.267)nm P=0.683 误差分析：从数据来看，仪器的精度很高，精确到小数点后第四位；相关系数很接近1，即线性程度很好；因此不确定度非常小。但是均值与真值有一定差距，原因可能是光点重合没有调好，图像不是非常清晰，影响观察，尤其是判断吞或吐出一个圆环的起始点时比较困难；还有仪器对外界条件的变化反应非常灵敏，因此外界干扰对实验的影响很大。