干涉法测微小量 陈泽亮.doc

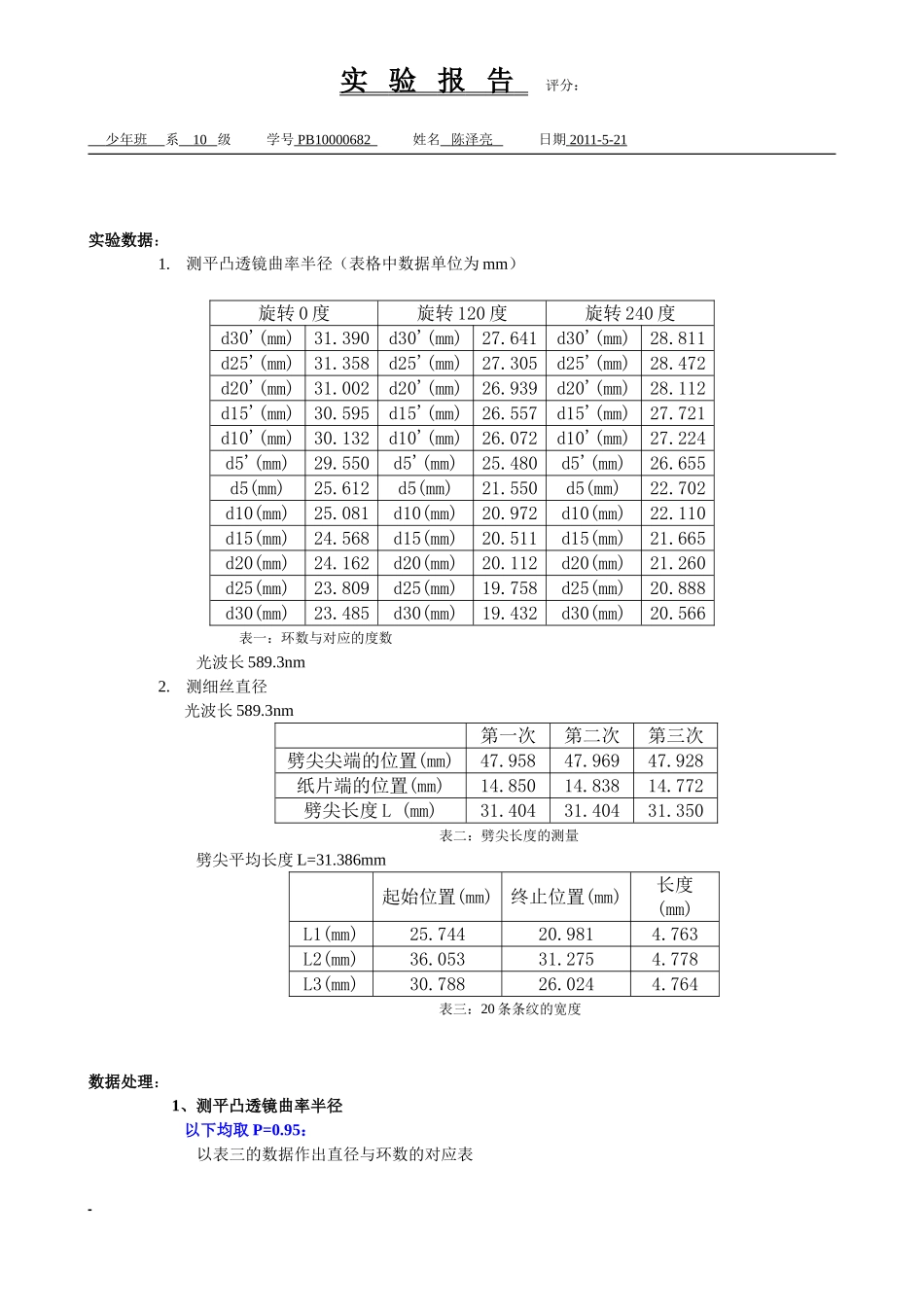
实 验 报 告 评分： 少年班 系 10 级 学号 PB10000682 姓名 陈泽亮 日期 2011-5-21 实验题目：干涉法测微小量 实验目的：学习、掌握利用光的干涉原理检验光学元件表面集合特征的方法，用劈尖的等厚干涉测量细丝直径的方法，同时加深对光的波动性的认识。 实验原理：1、用牛顿环测平凸透镜的曲率半径 当曲率很大的平凸透镜的凸面放在一平面玻璃上时，会产 生一组以O为中心的明暗相间的同心圆环，称为牛顿环。 如图，1、2两束光的光程差为，式中λ为入射光 的波长，δ是空气层厚度，空气折射率。如果第m个暗环处空气厚度为δm，则有 故得到：。 利用几何关系有，并根据，得到，联系以上两式，有 换成直径，并考虑第m+n个环和第m个环，有，，故 那么测量出Dm+n和Dm就可以根据这个表达式得到R。 2、劈尖的等厚干涉测细丝直径 两片叠在一起的玻璃片，在它们的一端夹一直径待测的细丝，于 是两玻璃片之间形成一空气劈尖。当用单色光垂直照射时，会产生干涉现象。因为程差相等的地方是平行于两玻璃片交线的直线，所以等厚干涉条纹是一组明暗相间、平行于交线的直线。 设入射光波为λ，则得第m级暗纹处空气劈尖的厚度。 由此可知，m=0时，d=0，即在两玻璃片交线处，为零级暗条纹。 如果在细丝处呈现m=N级条纹，则待测细丝直径。 3、利用干涉条纹检验光学表面面形 （略） 实验内容： 1． 测平凸透镜的曲率半径 （1） 观察牛顿环 1） 将牛顿环仪按图7.2.1-5所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方，木架上的透镜要正对着钠光灯窗口，调节玻璃片角度，使通过显微镜目镜观察时视场最亮。 2） 调节目镜，看清目镜视场的十字叉丝后，使显微镜筒下降到接近玻璃片，然后缓慢上升，直到观察到干涉条纹，再微调玻璃片角度及显微镜，使条纹更清楚。 （2） 测牛顿环直径 1） 使显微镜的十字叉丝交点与牛顿环中心重合，并使水平方向的叉丝与标尺平行（与显微镜筒移动方向平行）。 2） 转动显微镜测微鼓轮，使显微镜筒沿一个方向移动，同时数出十字叉丝竖丝移过的暗环数，直到竖丝与第35环相切为止。 3） 反向转动鼓轮，当竖丝与第30环相切时，记录读数显微镜上的位置读数d30，然后继续转动鼓轮，使竖丝依次与第25、20、15、10、5环相切，顺次记下读数d25，d20，d15，d10，d5。 4） 继续转动鼓轮，越过干涉圆环中心，记下竖丝依次与另一边的5、10、15、20、25、30环相切时的读数、、、、、。 重复测量三次，共测三组数据。 （3） 用逐差法处理数据 第30环的直径，同理，可求出D25、D20…D5，式（7）中，取n=15，求出，代入式计算R和R的标准差。 2． 测细丝直径 （1） 观察干涉条纹 将劈尖盒放在曾放置牛顿环的位置，同前法调节，观察到干涉条纹，使条纹最清晰。 （2） 测量 1） 调整显微镜及劈尖盒的位置，当转动测微鼓轮使镜筒移动时，十字叉丝的竖丝要保持与条纹平行。 2） 在劈尖玻璃面的三个不同部分，测出20条暗纹的总长度，测三次求其平均值及单位长度的干涉条纹数。 3） 测劈尖两玻璃片交线处到夹细线处的总长度L，测三次，求平均值。 4） 由公式，求细丝直径 实验数据： 1. 测平凸透镜曲率半径（表格中数据单位为mm） 旋转0度 旋转120度 旋转240度 d30'(mm) 31.390 d30'(mm) 27.641 d30'(mm) 28.811 d25'(mm) 31.358 d25'(mm) 27.305 d25'(mm) 28.472 d20'(mm) 31.002 d20'(mm) 26.939 d20'(mm) 28.112 d15'(mm) 30.595 d15'(mm) 26.557 d15'(mm) 27.721 d10'(mm) 30.132 d10'(mm) 26.072 d10'(mm) 27.224 d5'(mm) 29.550 d5'(mm) 25.480 d5'(mm) 26.655 d5(mm) 25.612 d5(mm) 21.550 d5(mm) 22.702 d10(mm) 25.081 d10(mm) 20.972 d10(mm) 22.110 d15(mm) 24.568 d15(mm) 20.511 d15(mm) 21.665 d20(mm) 24.162 d20(mm) 20.112 d20(mm) 21.260 d25(mm) 23.809 d25(mm) 19.758 d25(mm) 20.888 d30(mm) 23.485 d30(mm) 19.432 d30(mm) 20.566 表一：环数与对应的度数 光波长589.3nm 2. 测细丝直径 光波长589.3nm 　 第一次 第二次 第三次 劈尖尖端的位置(mm) 47.958 47.969 47.928 纸片端的位置(mm) 14.850 14.838 14.772 劈尖长度L (mm) 31.404 31.404 31.350 表二：劈尖长度的测量 劈尖平均长度L=31.386mm 　 起始位置(mm) 终止位置(mm) 长度(mm) L1(mm) 25.744 20.981 4.763 L2(mm) 36.053 31.275 4.778 L3(mm) 30.788 26.024 4.764 表三：20条条纹的宽度 数据处理： 1、测平凸透镜曲率半径 以下均取P=0.95： 以表三的数据作出直径与环数的对应表 并由公式计算出标准差 单位/mm 第一次 第二次 第三次 平均 标准差 D30 7.905 8.209 8.245 8.120 0.187 D25 7.549 7.547 7.584 7.560 0.021 D20 6.840 6.827 6.852 6.840 0.013 D15 6.027 6.046 6.056 6.043 0.015 D10 5.051 5.100 5.114 5.088 0.033 D5 3.938 3.930 3.953 3.940 0.012 表四：直径与对应环数的关系 展伸不确定度 利用逐差法处理上述数据。根据前述公式，则不确定度的传递公式应该是 取n=15得： =213.5mm =32.4mm =14.1mm 对以上值取平均： 同时由不确定度传递公式有： 故最终结果表示成： 分析：从计算结果看出R的不确定度相当大，寻找发现D30的标准差很大，原因可能是在试验中读数除了问题或者环数相差1-2环。 2、测纸片厚度 以下均取P=0.95： 劈尖长度 展伸不确定度： 20条条纹宽度平均值 展伸不确定度： 那么 由不确定度传递公式有： 于是最终结果写成 实验小结： 1、数牛顿环和条纹时眼睛易疲劳，容易数错，考验细心和耐心； 2、靠近中心区域条纹粗大，测量时，十字叉丝应该尽量处在环纹圈的径向中点处，而在测量远离中心区域的暗环数据时，由于暗环逐渐变细则只能做到与其明显界限相切，以缩小误差。 3、实验中应特别注意回程差的影响，测量时一旦开始向某个方向转动读数显微镜，就一定要保证本次测量绝对不能向反方向转，否者回转时的一部分读数会造成误差； 4、测量纸片的干涉条纹时，干涉条纹是不完全一样的。靠近纸片的一部分条纹是倾斜的，因此测量20条条纹的长度时必须选取较有代表性的条纹。 5、实验中容易出现操作失误，如实验中D30的测量，由于操作失误导致不确定度相当大。 思考题： 1. 如图，从空气膜上下表面反射的光线相遇在D处发生相干，其光程差为 ， 为什么式（1）写 ？ 答：由于半径近1m ，而BO只有几个毫米，故夹角极小，最多只有 ，于是空气层的上下两表面可以看作平行平面，此时： 所以 2. 牛顿环的中心级次是多少？是亮斑还是暗斑？你实验时牛顿环中心是亮还是暗？为什么？ 答：牛顿环的中心级次为 0 ，为暗斑。实际操作时确实观察到了暗斑，原因是 故 光程差为半波长的奇数倍，因而是暗斑。 且牛顿环中心是一个圆，原因在于在接近中心的区域中，所以暗斑为连续区域。 3. 为什么说在牛顿环和劈尖的实验中测量的干涉条纹数越多，测量的精度越高？ 答：在这两个实验中，干涉条纹并不是完全均匀的。增大测量的干涉条纹的数量，可以减少条纹不均匀带来的误差，提高测量的精度。