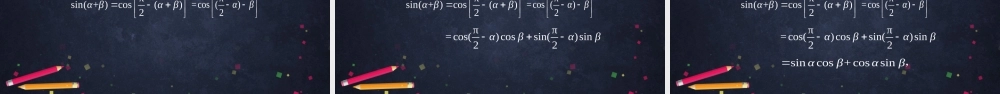0527高一数学（人教B版）-两角和与差的正弦、正切（第一课时）-2PPT课件【公众号悦过学习分享】.pptx.pptxVIP免费

高一年级数学两角和与差的正弦、正切(第一课时)主讲人徐艳玲北京市房山区良乡中学一、温故知新1.诱导公式二一、温故知新1.诱导公式二sin()sincos()costan()tan.αααααα，，一、温故知新2.诱导公式五一、温故知新2.诱导公式五πsin()cos2πcos()sin.2αααα，一、温故知新3.两角差的余弦公式一、温故知新3.两角差的余弦公式cos()coscossinsin.αβαβαβ二、探究新知尝试与发现二、探究新知(1)3045，怎样借助的三角函数值求出尝试与发现sin75sin15，的值？二、探究新知(1)3045，怎样借助的三角函数值求出尝试与发现sin75sin15，的值？sin75sin9015（）二、探究新知(1)3045，怎样借助的三角函数值求出尝试与发现sin75sin15，的值？sin75sin9015（）cos15二、探究新知(1)3045，怎样借助的三角函数值求出尝试与发现sin75sin15，的值？sin75sin9015（）cos4530（）cos15二、探究新知(1)3045，怎样借助的三角函数值求出尝试与发现sin75sin15，的值？6+2.4sin75sin9015（）cos4530（）cos15二、探究新知尝试与发现(2)αβ，一般地怎样根据与的三角函数值求出sin+sinαβαβ（），（）的值？二、探究新知尝试与发现根据两角和与差的余弦公式,可以证明如下的两角和与差的正弦公式.二、探究新知尝试与发现根据两角和与差的余弦公式,可以证明如下的两角和与差的正弦公式.Ssin()sincoscossinα+βα+βαβ+αβ：，二、探究新知尝试与发现根据两角和与差的余弦公式,可以证明如下的两角和与差的正弦公式.Ssin()sincoscossinα+βα+βαβ+αβ：，Ssin()sincoscossin.αβαβαβαβ：二、探究新知证明由诱导公式以及两角和与差的余弦公式可知二、探究新知证明由诱导公式以及两角和与差的余弦公式可知πsin(+)cos()2αβαβ二、探究新知证明由诱导公式以及两角和与差的余弦公式可知πsin(+)cos()2αβαβπ=cos()2αβ二、探究新知证明由诱导公式以及两角和与差的余弦公式可知πsin(+)cos()2αβαβπ=cos()2αβππ=cos()cossin()sin22αβαβ二、探究新知证明由诱导公式以及两角和与差的余弦公式可知πsin(+)cos()2αβαβπ=cos()2αβ...