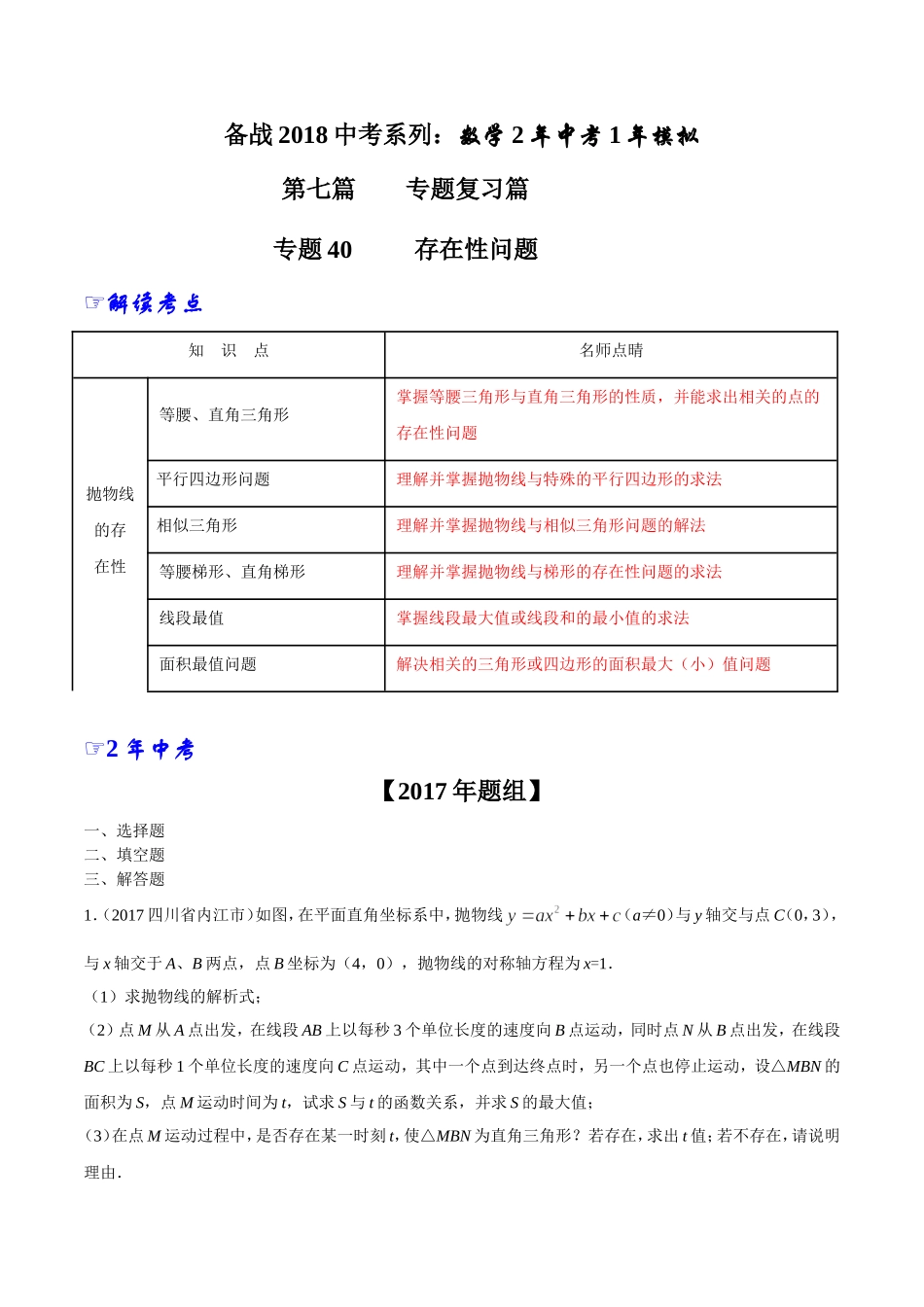
备战2018中考系列:数学2年中考1年模拟第七篇专题复习篇专题40存在性问题☞解读考点知识点名师点晴抛物线的存在性等腰、直角三角形[来源:学科网ZXXK][来源:学科网ZXXK][来源:学科网ZXXK]掌握等腰三角形与直角三角形的性质,并能求出相关的点的存在性问题[来源:Z§xx§k.Com][来源:学*科*网]平行四边形问题理解并掌握抛物线与特殊的平行四边形的求法相似三角形理解并掌握抛物线与相似三角形问题的解法等腰梯形、直角梯形理解并掌握抛物线与梯形的存在性问题的求法线段最值掌握线段最大值或线段和的最小值的求法面积最值问题解决相关的三角形或四边形的面积最大(小)值问题☞2年中考【2017年题组】一、选择题二、填空题三、解答题1.(2017四川省内江市)如图,在平面直角坐标系中,抛物线(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.(1)求抛物线的解析式;(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.【答案】(1);(2)S=,运动1秒使△PBQ的面积最大,最大面积是;(3)t=或t=.【解析】(3)根据余弦函数,可得关于t的方程,解方程,可得答案.试题解析:(1) 点B坐标为(4,0),抛物线的对称轴方程为x=1,∴A(﹣2,0),把点A(﹣2,0)、B(4,0)、点C(0,3),分别代入(a≠0),得:,解得:,所以该抛物线的解析式为:;(2)设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.由题意得,点C的坐标为(0,3).在Rt△BOC中,BC==5.如图1,过点N作NH⊥AB于点H,∴NH∥CO,∴△BHN∽△BOC,∴,即,∴HN=t,∴S△MBN=MB•HN=(6﹣3t)•t,即S==,当△PBQ存在时,0<t<2,∴当t=1时,S△PBQ最大=.答:运动1秒使△PBQ的面积最大,最大面积是;(3)如图2,在Rt△OBC中,cos∠B=.设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.①当∠MNB=90°时,cos∠B=,即,化简,得17t=24,解得t=;②当∠BMN=90°时,cos∠B=,化简,得19t=30,解得t=.综上所述:t=或t=时,△MBN为直角三角形.考点:1.二次函数综合题;2.最值问题;3.二次函数的最值;4.动点型;5.存...