1_4.2　导数的应用（分层集训）.pptx

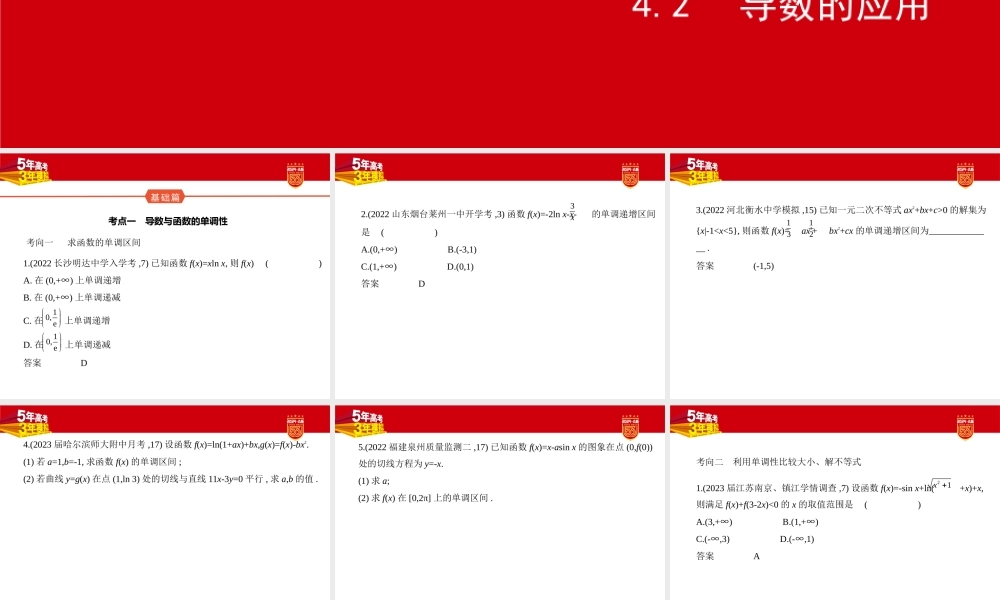
高考数学,专题四导数及其应用4.2导数的应用,考点一导数与函数的单调性,考向一 求函数的单调区间,1.(2022长沙明达中学入学考,7)已知函数f(x)=xln x,则f(x)()A.在(0,+)上单调递增B.在(0,+)上单调递减C.在上单调递增D.在上单调递减答案D,2.(2022山东烟台莱州一中开学考,3)函数f(x)=-2ln x-x-的单调递增区间是()A.(0,+)B.(-3,1)C.(1,+)D.(0,1)答案D,3.(2022河北衡水中学模拟,15)已知一元二次不等式ax2+bx+c0的解集为x|-1x5,则函数f(x)=ax3+bx2+cx的单调递增区间为.答案(-1,5),4.(2023届哈尔滨师大附中月考,17)设函数f(x)=ln(1+ax)+bx,g(x)=f(x)-bx2.(1)若a=1,b=-1,求函数f(x)的单调区间;(2)若曲线y=g(x)在点(1,ln 3)处的切线与直线11x-3y=0平行,求a,b的值.解析(1)由题意知f(x)=ln(1+x)-x,定义域为(-1,+),求导得f(x)=-1=,令f(x)=0,得x=0,当-10,当x0时,f(x)0,所以f(x)的单调递增区间为(-1,0),单调递减区间为(0,+).(2)g(x)=f(x)-bx2=ln(1+ax)+bx-bx2,求导得g(x)=+b-2bx,因为曲线y=g(x)在点(1,ln 3)处的切线与直线11x-3y=0平行,所以g(1)=,+b-2b=,g(1)=ln(1+a)+b-b=ln 3,解得a=2,b=-3.,5.(2022福建泉州质量监测二,17)已知函数f(x)=x-asin x的图象在点(0,f(0)处的切线方程为y=-x.(1)求a;(2)求f(x)在0,2上的单调区间.解析(1)对f(x)=x-asin x求导得f(x)=1-acos x,则f(0)=1-acos 0=1-a,根据f(x)=x-asin x的图象在(0,f(0)处的切线方程为y=-x,有1-a=-1,解得a=2.(2)由(1)可得f(x)=1-2cos x.在区间0,2上,由f(x)=0,解得x=或x=.当00,则f(x)单调递增.,综上可得,f(x)的单调递减区间为,单调递增区间为.,考向二利用单调性比较大小、解不等式,1.(2023届江苏南京、镇江学情调查,7)设函数f(x)=-sin x+ln(+x)+x,则满足f(x)+f(3-2x)0的x的取值范围是()A.(3,+)B.(1,+)C.(-,3)D.(-,1)答案A,2.(2021湖南郴州质检三,8)已知a=4ln 3,b=3ln 4,c=4ln 3,则a,b,c的大小关系是()A.cbaB.bcaC.bacD.abc答案B,3.(2022河北邯郸二模,8)已知函数f(x)=ln x,且a=f,b=f,c=f(),则()A.abcB.cabC.acbD.cba答案B,4.(2022全国甲文,12,5分)已知9m=10,a=10m-11,b=8m-9,则()A.a0bB.ab0C.ba0D.b0a答案A,5.(2022广东汕头一模,5)已知a=,b=,c=,则以下不等式正确的是()A.cbaB.abcC.bacD.bca答案C,6.(2023届广东六校联考,16)若不等式a(x+1)ex-x0有且仅有一个正整数解,则实数a的取值范围是.答案,考点二导数与函数的极(最)值,1.(2023届江西上饶、景德镇六校联考,11)设a0,若x=a为函数f(x)=a(x-a)2(x-1)的极小值点,则()A.a1C.aa2答案C,2.(2022海南海口四中期中,14)若函数f(x)=-x3+ax2-4在x=2处取得极值,则a=.答案3,