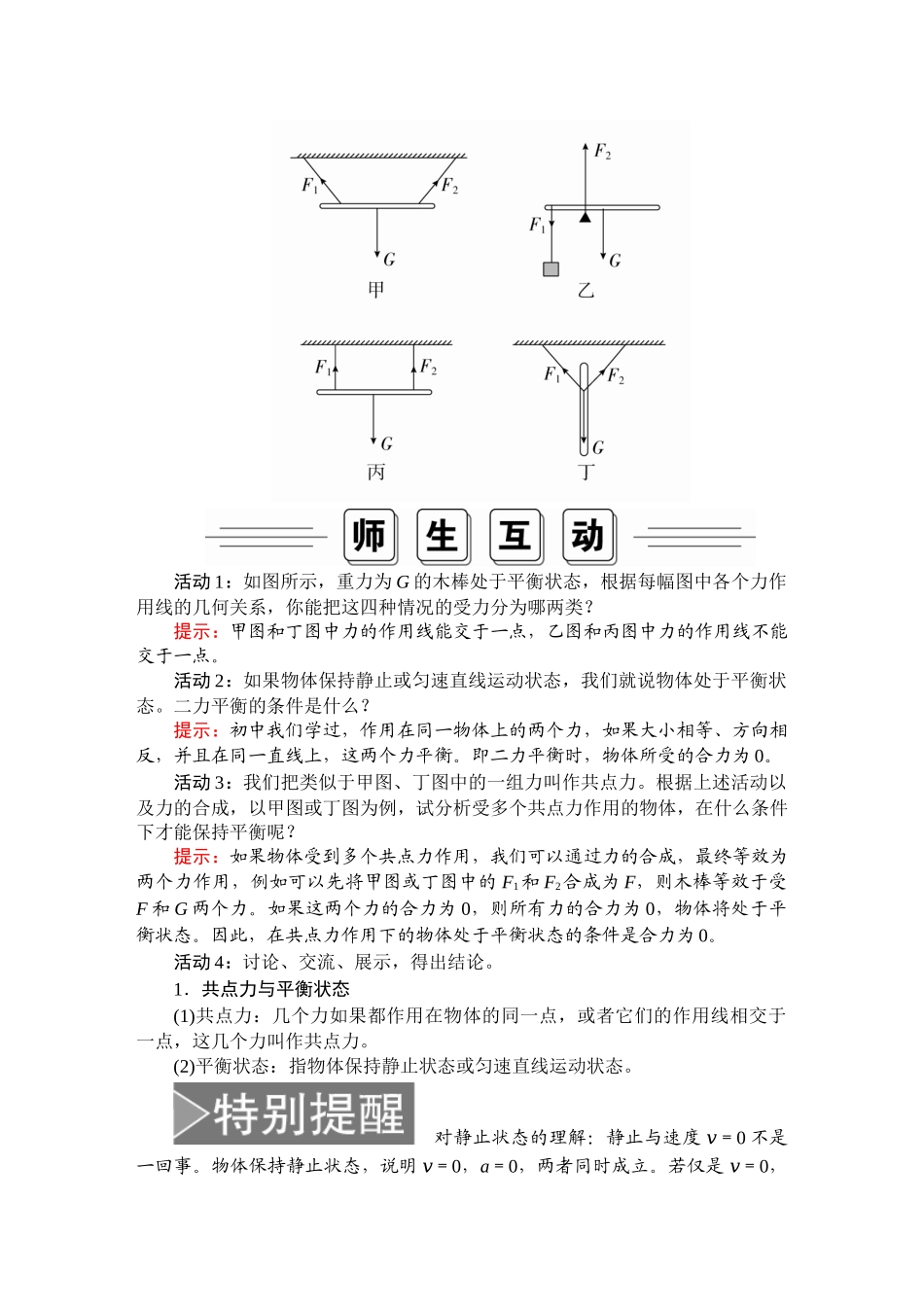
5.共点力的平衡1.理解共点力作用下物体处于平衡状态的含义以及物体在共点力作用下平衡的条件。2.会用共点力平衡的条件解决有关共点力的平衡问题。一、共点力1.定义:几个力如果都作用在物体的□同一点,或者它们的□作用线相交于一点,这几个力叫作共点力。2.力的合成和分解的平行四边形定则,只适用于□共点力。二、共点力平衡的条件1.平衡状态物体在力的作用下保持的□静止或□匀速直线运动状态。2.共点力平衡的条件:在共点力作用下物体平衡的条件是□合力为0。判一判(1)共点力一定作用于物体上的同一点。()(2)共点力一定作用于同一物体上。()(3)作用于同一物体上的所有的力都是共点力。()(4)平直道路上高速匀速行驶的赛车处于平衡状态。()(5)百米竞赛中,运动员在起跑时速度为零的瞬间处于平衡状态。()(6)合力保持恒定的物体处于平衡状态。()提示:(1)×共点力不一定作用于物体上的同一点,也可能是共点力的作用线交于一点。(2)√共点力一定作用于同一物体上。(3)×作用于同一物体上的力不一定是共点力,也可能是平行力。(4)√赛车沿平直道路高速匀速行驶,合力为零,故赛车处于平衡状态。(5)×运动员起跑瞬间虽然速度为零,但具有加速度,不处于平衡状态。(6)×当合力恒定且不为零时,物体的速度会发生变化,物体不处于平衡状态。想一想当物体的速度为零时,是否一定处于平衡状态?提示:不一定,如物体做自由落体运动的初始时刻速度为零,但合外力不为零,物体没有处于平衡状态。课堂任务共点力及共点力的平衡条件仔细观察下列图片,认真参与“师生互动”。活动1:如图所示,重力为G的木棒处于平衡状态,根据每幅图中各个力作用线的几何关系,你能把这四种情况的受力分为哪两类?提示:甲图和丁图中力的作用线能交于一点,乙图和丙图中力的作用线不能交于一点。活动2:如果物体保持静止或匀速直线运动状态,我们就说物体处于平衡状态。二力平衡的条件是什么?提示:初中我们学过,作用在同一物体上的两个力,如果大小相等、方向相反,并且在同一直线上,这两个力平衡。即二力平衡时,物体所受的合力为0。活动3:我们把类似于甲图、丁图中的一组力叫作共点力。根据上述活动以及力的合成,以甲图或丁图为例,试分析受多个共点力作用的物体,在什么条件下才能保持平衡呢?提示:如果物体受到多个共点力作用,我们可以通过力的合成,最终等效为两个力作用,例如可以先将甲图或丁图中的F1和F2合成为F,则木棒等效于受F和G两个力。如果这两个...