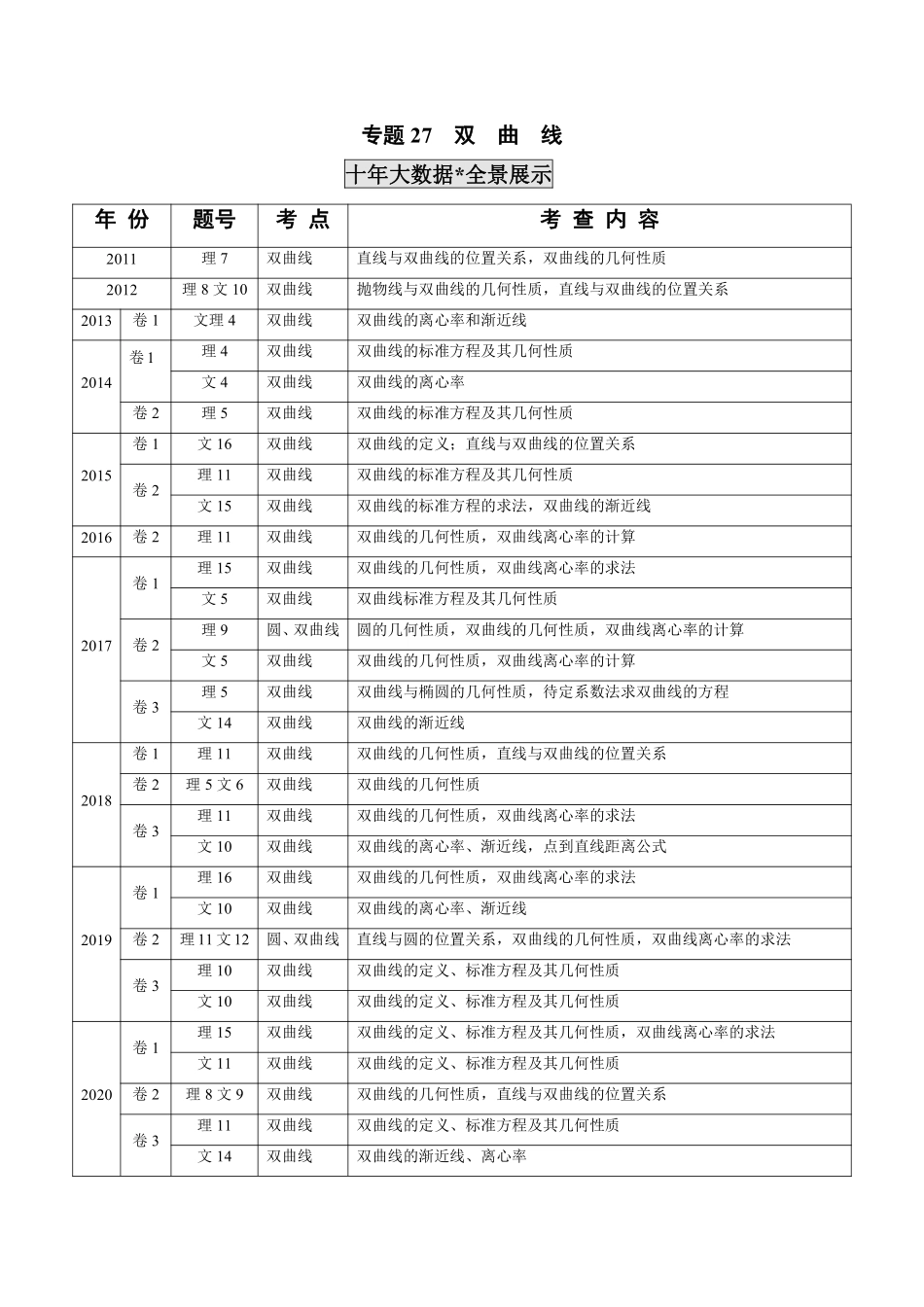
专题27双曲线十年大数据*全景展示年份题号考点考查内容2011理7双曲线直线与双曲线的位置关系,双曲线的几何性质[来源:学&科&网Z&X&X&K]2012理8文10双曲线抛物线与双曲线的几何性质,直线与双曲线的位置关系2013卷1文理4双曲线双曲线的离心率和渐近线2014卷1[来源:学.科.网][来源:Z.xx.k.Com][来源:Zxxk.Com]理4双曲线[来源:学。科。网]双曲线的标准方程及其几何性质文4双曲线双曲线的离心率卷2理5双曲线双曲线的标准方程及其几何性质2015卷1文16双曲线双曲线的定义;直线与双曲线的位置关系卷2理11双曲线双曲线的标准方程及其几何性质文15双曲线双曲线的标准方程的求法,双曲线的渐近线2016卷2理11双曲线双曲线的几何性质,双曲线离心率的计算2017卷1理15双曲线双曲线的几何性质,双曲线离心率的求法文5双曲线双曲线标准方程及其几何性质卷2理9圆、双曲线圆的几何性质,双曲线的几何性质,双曲线离心率的计算文5双曲线双曲线的几何性质,双曲线离心率的计算卷3理5双曲线双曲线与椭圆的几何性质,待定系数法求双曲线的方程文14双曲线双曲线的渐近线2018卷1理11双曲线双曲线的几何性质,直线与双曲线的位置关系卷2理5文6双曲线双曲线的几何性质卷3理11双曲线双曲线的几何性质,双曲线离心率的求法文10双曲线双曲线的离心率、渐近线,点到直线距离公式2019卷1理16双曲线双曲线的几何性质,双曲线离心率的求法文10双曲线双曲线的离心率、渐近线卷2理11文12圆、双曲线直线与圆的位置关系,双曲线的几何性质,双曲线离心率的求法卷3理10双曲线双曲线的定义、标准方程及其几何性质文10双曲线双曲线的定义、标准方程及其几何性质2020卷1理15双曲线双曲线的定义、标准方程及其几何性质,双曲线离心率的求法文11双曲线双曲线的定义、标准方程及其几何性质卷2理8文9双曲线双曲线的几何性质,直线与双曲线的位置关系卷3理11双曲线双曲线的定义、标准方程及其几何性质文14双曲线双曲线的渐近线、离心率大数据分析*预测高考考点出现频率2021年预测考点92双曲线的定义及标准方程23次考2次命题角度:(1)双曲线的定义及应用;(2)双曲线的标准方程;(3)双曲线的几何性质.核心素养:直观想象、数学运算考点93双曲线的几何性质23次考21次考点94直线与双曲线的位置关系23次考5次十年试题分类*探求规律考点92双曲线的定义及标准方程1.(2017新课标Ⅲ理)已知双曲线C:22221(0,0)xyabab的一条渐近线方程为52yx,且与椭圆221123xy有公共焦点,则C的方程为A.2...